Volumen de cuerpos geométricos

1- Volumen de un cuerpo geométrico

El volumen (V) de un cuerpo es la medida del espacio que ocupa.

La capacidad es la medida del volumen que puede contener un cuerpo.

Como en general estas medidas son iguales, se suele calcular la capacidad mediante la fórmula del volumen.

La medida universal del volumen es el metro cúbico (m³), existiendo los múltiplos y submúltiplos de esta medida.

Para calcular el volumen de un cubo de arista 1 m, se multiplica la medida del ancho por el largo y por el alto:

El volumen del cubo es 1 m³ (un metro cúbico).

 

 

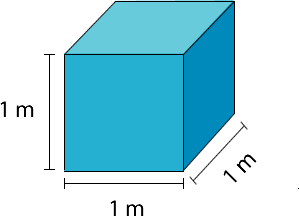
De la misma forma, se puede representar el centímetro cúbico (cm³), el decímetro cúbico (dm³), el milímetro cúbico (mm³), entre otros.

Veamos un ejemplo de cálculo de volumen.

El volumen de cada cubo es de 1m³, ¿cuál es el volumen del cuerpo expresado en m³?

En este caso se puede calcular el volumen del cuerpo, contando la cantidad total de cubos que lo conforman.

 

 

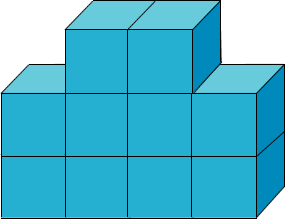
El volumen del cuerpo es de 10 m³.

 

2- Volumen de un prisma recto

Un prisma es un poliedro, cuyas caras son paralelogramos. Las bases de los prismas son paralelas y congruentes.

Como vimos en el punto anterior, se puede calcular el volumen de un cuerpo geométrico, contando la cantidad de unidades cúbicas que caben dentro de él.

 

 

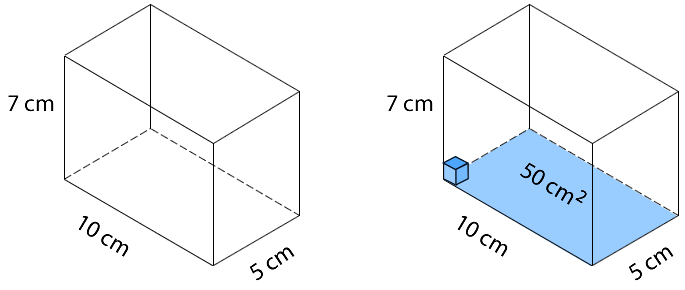
Observamos que la base es un rectángulo de $10 · 5$, entonces se pueden cubrir con 50 cubos de arista 1 cm.

Posteriormente, observamos la medida de la altura, que es equivalente a 7 cm. Entonces, hay 7 capas de 50 cubos cada una.

El volumen del prisma está dado por:

$$\begin{gathered} V=10 · 5 · 7 \\ V=350 c{m}^3 \end{gathered}$$

Como puedes ver, primero se calculó el área de la base del prisma y posteriormente su resultado se multiplicó por la medida de la altura. Esto se puede expresar mediante la siguiente fórmula:

 

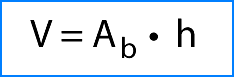
A_b= área basal del prisma.
h = altura del prisma.

Esta fórmula se puede aplicar para calcular el volumen de un prisma recto cualquiera.

Ejemplo 1: Prisma recto de base rectangular.

 

 

$$\begin{gathered} A_b = 5· 3 \\ {A}_b = 15 c{m}^2 \end{gathered}$$

$$\begin{gathered} V = A_b· h \\ V =\hspace{0.17em}15 ·8 \\ V= 120 c{m}^3 \end{gathered}$$

 

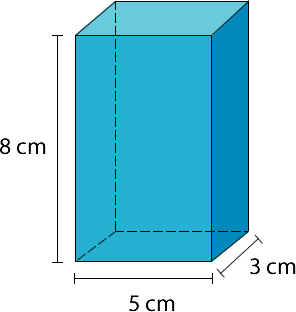
Ejemplo 2: Prisma recto de base triangular.

 

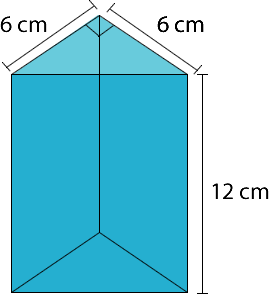
Calculamos el área de la base. Recordemos que el área del triángulo se calcula multiplicando la medida de la base por la altura y se divide por 2.
 

$$\begin{gathered} A_b = \frac{6 · 6}{2}=\frac{36}{2}=18 c{m}^2 \\ {A}_b = 18 c{m}^2 \end{gathered}$$
Reemplazamos los datos en la fórmula:

$$\begin{gathered} V = A_b· h \\ V =\hspace{0.17em}18 ·12 \\ V= 216 c{m}^3 \end{gathered}$$

 

Ejemplo 3: Prisma pentagonal recto.

 

 

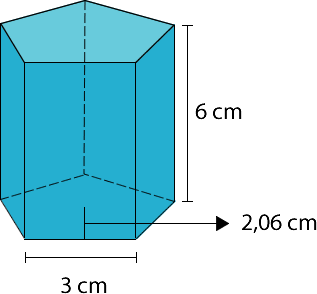
En este caso, la base del prisma es un pentágono regular. Para calcular el área de un polígono regular emplearemos la siguiente fórmula:

 

 

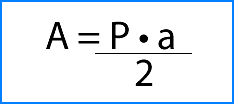
P = perímetro
a = apotema

La apotema de un polígono regular es el segmento que une el centro del polígono con cualquiera de sus lados.

El perímetro del polígono de la base es: $5 · 3 =15 cm$

Ahora reemplazamos los otros datos:
$$\begin{gathered} A=\frac{15 · 2,06}{2} \\ A=15,45 c{m}^2 \end{gathered}$$

Reemplazamos los datos en la fórmula de volumen de un prisma:

$$\begin{gathered} V = A_b· h \\ V =\hspace{0.17em}15,45 ·6 \\ V= 92,7 c{m}^3 \end{gathered}$$

 

3- Volumen de una pirámide

La pirámide es un poliedro que tiene caras laterales triangulares y su base es un polígono.

Consideremos un prisma de base rectangular lleno de agua.

Si se vaciara el agua contenida en el prisma de base rectangular en pirámides que tienen la misma base y altura, podemos determinar que  el volumen de una pirámide es igual a un tercio del volumen del prisma.

Entonces, para calcular el volumen de una pirámide regular, se puede calcular el volumen de un prisma  (igual base y altura) y posteriormente se divide el resultado por 3.
 

 

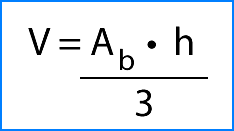
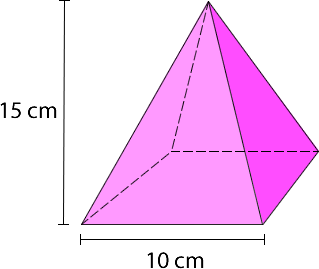
Ejemplo 1: Pirámide de base cuadrada.

 

 

$$\begin{gathered} A_b=10 · 10 \\ {A}_b=100 c{m}^2 \end{gathered}$$
 

$$\begin{gathered} V = \frac{A_b· h}{3} \\ V =\hspace{0.17em}\frac{100 ·15}{3} \\ V=500 c{m}^3 \end{gathered}$$

 

Ejemplo 2: Pirámide pentagonal regular recta.

 

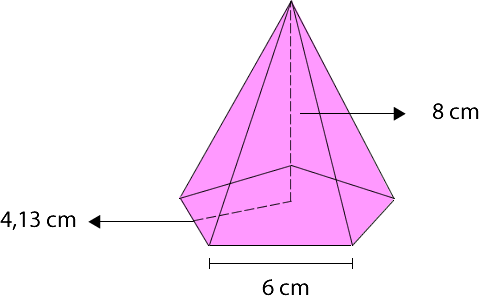
En este caso, la base de la pirámide es un pentágono regular. Aplicamos la fórmula para determinar el área de la base.

 

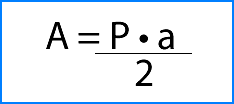
El perímetro del polígono de la base es:

$$\begin{gathered} P =5 · 6 \\ P = 30 cm \end{gathered}$$

 

$$\begin{gathered} A=\frac{30 · 4,13}{2} \\ A=61,95 c{m}^2 \end{gathered}$$

Reemplazamos los datos en la fórmula de volumen:
 

$$\begin{gathered} V = \frac{A_b· h}{3} \\ V =\hspace{0.17em}\frac{61,95 ·8}{3} \\ V=165,2 c{m}^3 \end{gathered}$$

 

4- Volumen del cilindro

Un cilindro es un cuerpo redondo o cuerpo de rotación.
Si se hace girar un rectángulo sobre uno de sus lados se puede obtener la siguiente figura:

 

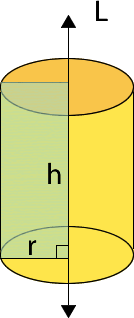
h= altura
r= radio
L= eje de rotación

El volumen del cilindro se asemeja al de un prisma, por lo que se puede calcular determinando el área de la base y posteriormente el resultado se multiplica por la medida de la altura.

$V =\hspace{0.17em}{A}_b · h$

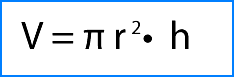
r= radio de la base
h= altura del cilindro.

Ejemplo:

 

 

$$\begin{gathered} V =\hspace{0.17em}{\mathrm{\pi r}}^2 · h \\ V =\hspace{0.17em}36\mathrm{\pi } ·12 \\ V =432\mathrm{\pi } c{m}^3 \end{gathered}$$
 

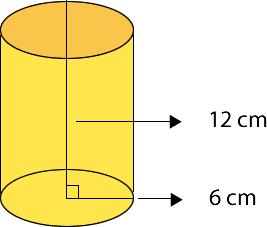
Si se considera $\mathrm{\pi }=3,14$, el volumen del cilindro es 1356,48 cm³.

5- Volumen del cono

El cono es un cuerpo redondo que se genera al rotar un triángulo rectángulo sobre uno de sus catetos.

 

 

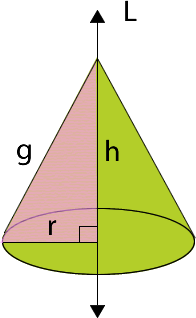
h = altura
g = generatriz
r = radio
L = eje de rotación

La generatriz es la hipotenusa del triángulo rectángulo que genera la superficie del cono.

 

El volumen de un cilindro equivale a 3 veces el volumen del cono de igual base y altura, por lo que el volumen de cualquier cono recto está dado por la siguiente expresión:

 

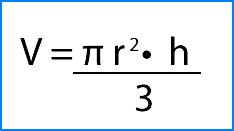
r= radio de la base
h= altura del cilindro.

Si el volumen de un cilindro es $90 \mathrm{\pi } {\mathrm{cm}}^3$, el volumen de un cono con su misma base y altura será  $30\mathrm{\pi } {\mathrm{cm}}^3$.

 

Ejemplo:

 

 

 

 

$$\begin{gathered} V =\hspace{0.17em}\frac{{\mathrm{\pi r}}^2 · h }{3} \\ V =\frac{\hspace{0.17em}9\mathrm{\pi } ·8}{3} \\ V =24\mathrm{\pi } c{m}^3 \end{gathered}$$

 

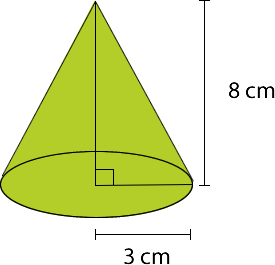
Si se considera  $\mathrm{\pi }=3,14$ el volumen es:
 

$$\begin{gathered} V= 24 ·3,14 \\ V=75,36 c{m}^3 \end{gathered}$$

 

6- Resumen
 

 

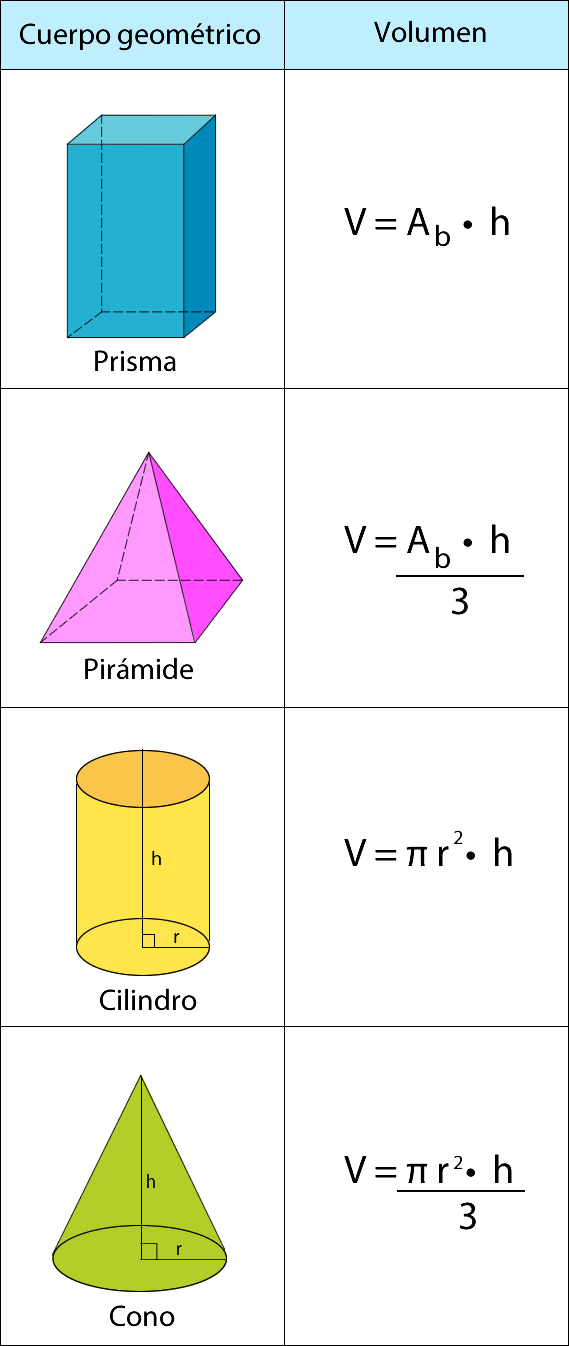
7- Resolución de problemas

1- El volumen de un prisma recto es 270 m³. Si su base es un rectángulo de lados 5 m y 6 m respectivamente, ¿cuánto mide la altura del prisma?

Conocemos la medida de la base del rectángulo, entonces calculamos su área:
 

$$\begin{gathered} A_b= 5 · 6 \\ {A}_b= 30 m^2 \end{gathered}$$

A continuación, reemplazamos los datos conocidos en la fórmula del volumen del prisma:

V = 270 m³
A_b = 30 m²

 

$$\begin{gathered} V =A_b · h \\ 270 =30· h \\ \frac{270}{30}=h \\ 9= h \end{gathered}$$

Respuesta: La altura del prisma es de 9 m.

 

2- En una empresa embalan cajas cúbicas cuyas aristas miden  0,5 m  en contenedores como el que se muestra en la imagen. ¿Cuál es la cantidad máxima de cajas que se pueden guardar en el contenedor?

 

 

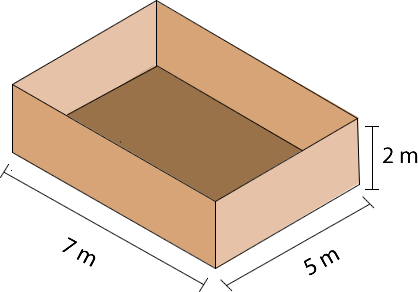
Para poder resolver este problema necesitamos saber el volumen del contenedor y de la caja cúbica.

Volumen contenedor:

$$\begin{gathered} V =\hspace{0.17em}7 · 5 ·2 \\ V=70 m^3 \end{gathered}$$

Volumen caja: 

$$\begin{gathered} V=0,5 · 0,5 · 0,5 \\ V= 0,125 m^3 \end{gathered}$$

 

Finalmente para obtener el mayor número de cajas que entrará en el contenedor dividimos los valores obtenidos:

$70 : 0,125 =\hspace{0.17em}560$

Respuesta: el mayor número de cajas que se pueden guardar en el contenedor son 560.

3- Si el área de la base de un prisma se duplica. ¿Cuánto aumenta su volumen?

Para conocer la variación del volumen, podemos atribuirle un valor al área basal y a la altura del prisma.

El área basal del primer prisma es 12 cm² y la altura de 10 cm. Si representamos el mismo prisma con su base duplicada, esta será equivalente a 24 cm² y su altura se mantiene.
 

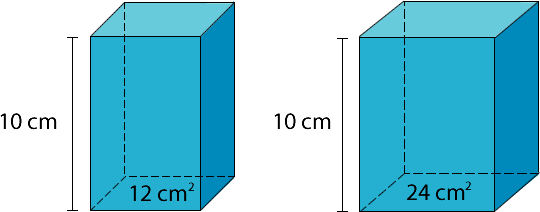
A continuación, se calculan los volúmenes de ambos prismas.
 

$$\begin{gathered} V =\hspace{0.17em}{A}_b · h \\ V =12 ·10 \\ V =\hspace{0.17em}120 c{m}^3 \\ V =\hspace{0.17em}{A}_b · h \\ V =24 ·10 \\ V =\hspace{0.17em}240 c{m}^3 \end{gathered}$$

Como se puede observar, si la base se duplica, su volumen también lo hará.

Respuesta: Si la base de un prisma se duplica, su volumen también lo hará.

4- Una cilindro tiene un diámetro de  6 cm y su altura es de 12 cm. ¿Cuál es su volumen? Considera $\mathrm{\pi }= 3,14.$

 

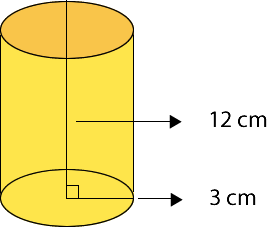
Los valores entregados son:

h = 12 cm
d = 6 cm

El radio corresponde a la mitad de la medida del diámetro, por lo que su valor es de 3 cm.
 

Los datos que se reemplazan en la fórmula son:
r= 3 cm, h= 12 cm y $\mathrm{\pi }$= 3,14

$$\begin{gathered} V =\hspace{0.17em}{\mathrm{\pi r}}^2 · h \\ \mathrm{V}=3,14 ·3^2 ·12 \\ \mathrm{V}=28,26 ·12 \\ \mathrm{V}=339,12 {\mathrm{cm}}^3 \end{gathered}$$

Respuesta: El volumen del cilindro es de 339,12 cm³.      
                              

5- Un cilindro tiene un volumen de 401,92 cm³. Si el diámetro de la base mide 8 cm, ¿cuánto mide la altura del cilindro? Considera  $\mathrm{\pi }=3,14.$

 

 

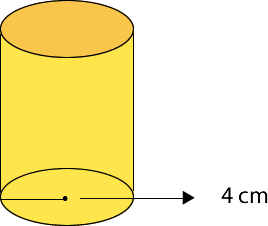
Para resolver este tipo de ejercicios, se deben reemplazar los valores conocidos en la fórmula del volumen del cilindro.

Los datos entregado son:
V= 401,92 cm³ y diámetro= 8 cm

Primero, se necesita saber el valor del radio que corresponde a la mitad del valor del diámetro. Por lo tanto, el valor del radio es equivalente a 4 cm.

Los datos que se reemplazarán en la fórmula son:

V= 401,92 cm³  y r= 4 cm y  $\mathrm{\pi }$=3,14

 

$$\begin{gathered} V =\hspace{0.17em}{\mathrm{\pi r}}^2 · h \\ 401,92=3,14 ·4^2 ·h \\ 401,92=50,24 ·h \\ \frac{401,92}{50,24} =h \\ 8 =\hspace{0.17em}h \end{gathered}$$

                                     
Respuesta: La altura del cilindro es igual a 8 cm.