Estudia

Practica

Pregunta

Trabajo y potencia

15 años > Física > Temperatura y calor

1.- Trabajo Mecánico

Primero recordemos el concepto de fuerza:

“Fuerza es todo aquello capaz de deformar un cuerpo o de variar su estado de reposo o de movimiento”

El efecto que una fuerza produce sobre un cuerpo depende de su magnitud, dirección y sentido, o sea, las fuerzas son vectores.

Si la fuerza logra desplazar un objeto, esa fuerza está produciendo que el cuerpo realice un trabajo mecánico, que es equivalente a la energía necesaria para desplazarlo.

“El trabajo es una magnitud escalar que es ocasionada cuando una fuerza mueve un cuerpo en su misma dirección”

Se dice que la fuerza realiza un trabajo cuando altera el estado de movimiento de un cuerpo. Si la fuerza que actúa en el objeto no produce un desplazamiento de este, no se realizó trabajo alguno.

Si la dirección de la fuerza no es paralela al desplazamiento, solo la componente de la fuerza que es paralela al desplazamiento será la que produzca el trabajo:

W = F \cdot \cos α \cdot ∆ \overset{⇀}{x}

Donde:

W =

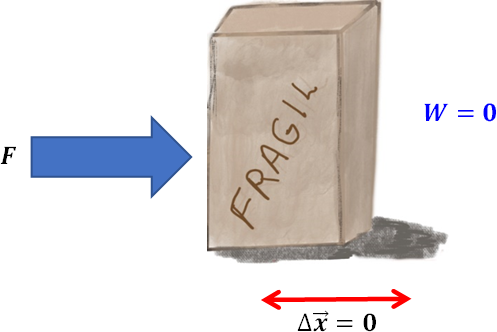
trabajo realizado, en

N \cdot m = J o u l e (J)

{\vec{F}}_{x} = \vec{F} \cdot \cos α =

componente de la fuerza en la dirección del movimiento, Newtons

(N)

∆ \vec{x} =

desplazamiento en metros,

m

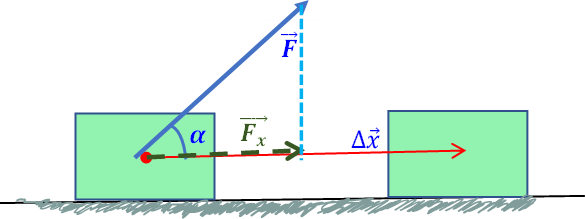
Si el ángulo $α$ vale $0 °$ , $\cos (0 °) = 1$ , ${\vec{F}}_{x} = \vec{F} c o s (0 °) = \vec{F}$ y entonces la ecuación se vuelve: $W = \vec{F} \cdot ∆ \vec{x}$ , pues la fuerza actúa en la misma dirección y sentido que el desplazamiento:

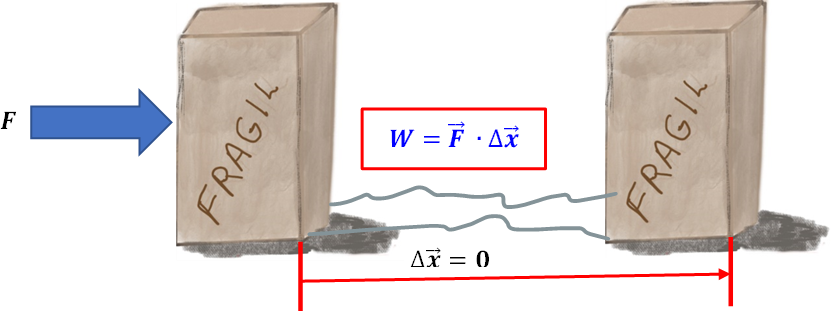
¿Qué ocurre si la fuerza es perpendicular al desplazamiento?

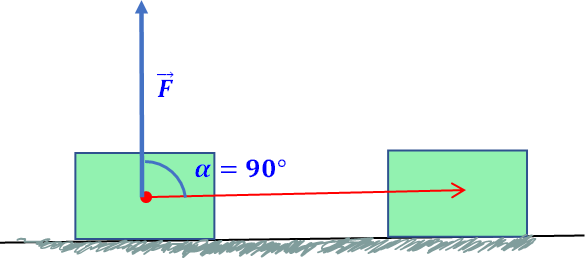
Si el ángulo $α$ vale $90 °$ , $c o s (90 °) = 0,$ y ${\vec{F}}_{x} = \vec{F} c o s (90 °) = 0$ , entonces: $W = 0$ , esto es, hubo un trabajo nulo, por ejemplo, el trabajo realizado por la fuerza del peso de una persona dirigida al piso, cuando esta se desplaza horizontalmente.

Una fuerza realizará un trabajo positivo o trabajo motor, siempre y cuando el ángulo, $α$ , entre la fuerza y el desplazamiento esté en el rango $0 ° \leq α < 90 °$ . (Ver los ejemplos 2 y 3)

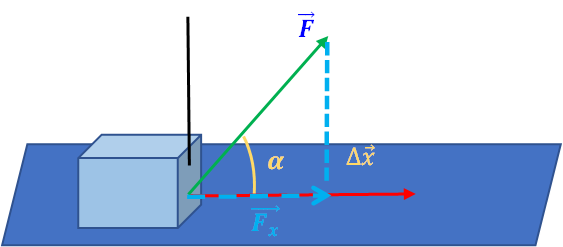
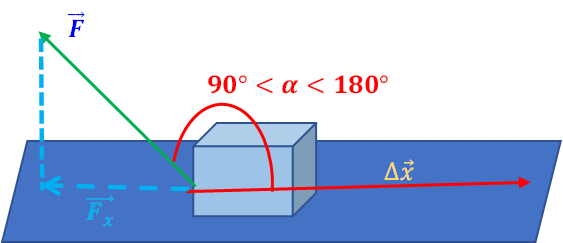
Una fuerza realizará un trabajo negativo o resistente siempre y cuando el ángulo, $α$ , entre la fuerza y el desplazamiento esté en el rango $90 ° < α \leq 180$ °. La componente de la fuerza paralela al movimiento tendrá la dirección opuesta al mismo, pues el coseno del ángulo va a ser negativo y, por esto, reducirá el desplazamiento.

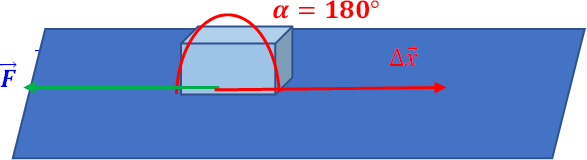
Para el caso en que el ángulo sea $180 °$ , $\vec{F} < 0$ , la fuerza se opondrá totalmente al desplazamiento realizado por el cuerpo, por ejemplo, en el caso de la fricción con el piso.

A pesar de que tanto la fuerza como el desplazamiento son vectores, el trabajo es una magnitud escalar.

La unidad de medida del trabajo para el SI es el Joule (J), que se define como el trabajo realizado por una fuerza constante de 1 Newton que actúa sobre un cuerpo, provocando un desplazamiento de 1 metro en la misma dirección y sentido que la fuerza actuante, de donde:

$1 J = 1 N \cdot m$

Habrá ocasiones en las que varias fuerzas actúen sobre un cuerpo para producir un desplazamiento. En este caso, el trabajo total que recibe el cuerpo es la suma de los trabajos realizados por cada una de las fuerzas, o sea:

$W = W_{1} + W_{2} + W_{3} + . . . + W_{n}$

Y si, sustituimos la definición de trabajo en cada uno de los componentes de la ecuación, tendremos que:

$W = {\vec{F}}_{1} \cdot ∆ \vec{x} + {\vec{F}}_{2} \cdot ∆ \vec{x} + {\vec{F}}_{3 \cdot} ∆ \vec{x} + . . . + {\vec{F}}_{n \cdot} ∆ \vec{x}$

Y podemos factorizar el desplazamiento como factor común:

$W = ({\vec{F}}_{1} + {\vec{F}}_{2} + {\vec{F}}_{3} + . . . + {\vec{F}}_{n}) \cdot ∆ \vec{x}$

Y, si sustituimos la fuerza resultante ${\vec{F}}_{r}$ en lugar de la suma de fuerzas, tendremos:

$W = {\vec{F}}_{r} \cdot ∆ \vec{x}$

Si hacemos una gráfica de Fuerza constante contra desplazamiento, tal como la de la siguiente figura, el área indicada nos representa el trabajo realizado.

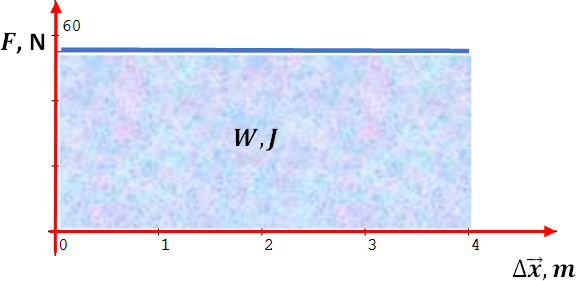
Por ejemplo, el trabajo realizado por $55$ Newtons de fuerza durante $4 m$ de desplazamiento será el área del rectángulo:

$Á r e a = b a s e \cdot a l t u r a$

$W = 4 \cdot 55 = 220 J$

Ejemplos:
1. En la siguiente figura vemos un cuerpo cuyo peso es de $10 N$ y se levanta a una altura de $1 m$ . ¿A cuánto equivale el trabajo realizado?

Datos:
$F = 10 N$
$∆ \vec{x} = 1 m$
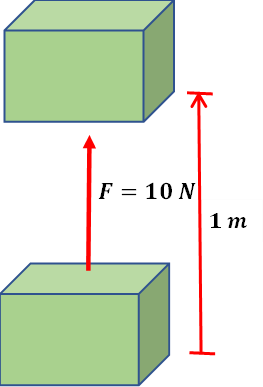$α = 0 °$ respecto a la línea de desplazamiento

Y sustituyendo en la ecuación que define el trabajo:

$W = F \cdot \cos α \cdot ∆ \vec{x}$

$W = 10 \cdot \cos (0) \cdot 1 = 10 J$

El cuerpo realizó un trabajo de $10 J$ al subir un metro.

2. Si un cuerpo es empujado en forma horizontal con una fuerza de 3 N, suficiente para vencer la fuerza de fricción y desplazarlo $2 m$ con velocidad constante, ¿A cuánto es igual el trabajo realizado?

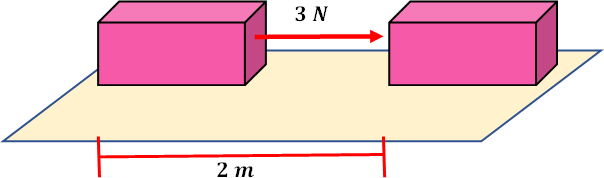
Datos:

$F = 3 N$
$∆ \vec{x} = 2 m$
$α = 0 °$ respecto a la línea de desplazamiento

Sustituyendo en la fórmula para calcular el trabajo, tenemos:

$W = F \cdot \cos α \cdot ∆ \vec{x} = 3 \cdot \cos (0 °) \cdot 2 = 6 J$

Así que el cuerpo realizó un trabajo de $6 J$

3. En la siguiente figura tenemos al mismo cuerpo, pero ahora es jalado por una fuerza de $6 N$ que forma un ángulo de $30 °$ respecto a la dirección del desplazamiento. ¿Cuál será el valor del trabajo realizado, si el desplazamiento del cuerpo es de $2 m$ ?

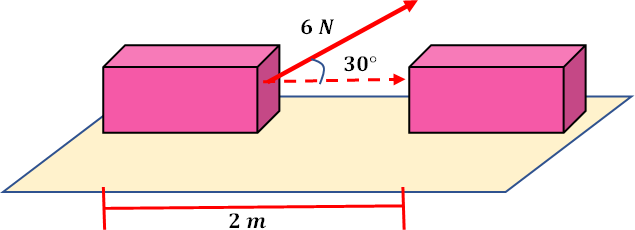
Al observar la figura, vemos que la fuerza de $6 N$ debe descomponerse para utilizar sólo su componente horizontal, que es la que ocasiona el desplazamiento, dado que el mismo es horizontal.

Datos:
$F = 3 N$
$∆ \vec{x} = 2 m$
$α = 30 °$ respecto a la línea de desplazamiento

Sustituyendo los datos en la ecuación que define trabajo, tenemos:

$W = F \cdot \cos α \cdot ∆ \vec{x} = 6 \cdot \cos (30 °) \cdot 2 = 6 \cdot 0, 8660 = 10, 39 J$

El trabajo realizado por el cuerpo será $10, 39 J$

4. Una persona cuyo peso es de $588 N$ sube por una escalera fijada en la pared que tiene una longitud de 17 metros, hasta llegar a una altura de 10 metros.

Calcula:
a. ¿Qué trabajo realizó?

b. Si la longitud de la escalera se mantiene, pero ahora está inclinada $30 °$ respecto a la vertical, ¿cuál será el trabajo realizado por la persona?

Respuestas:
a. La persona debe realizar una fuerza igual a su peso para alcanzar la altura de $10 m$ . Como la escalera está fijada a la pared, el movimiento será totalmente vertical, y el ángulo será $0 °$ . El desplazamiento realizado será la longitud de la escalera.

Datos:
$F = p e s o = 588 N$
$∆ \vec{x} = 10 m$
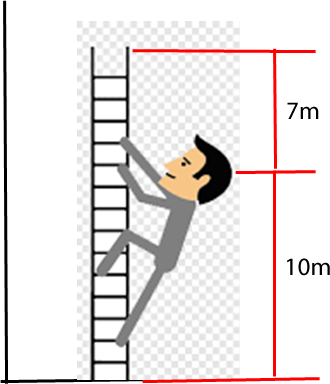$α = 0 °$ respecto a la dirección del movimiento

Sustituyendo los datos en la ecuación que define el trabajo:

$W = F \cdot \cos α \cdot ∆ \vec{x} W = 588 \cdot \cos (0 °) \cdot 10 W = 588 \cdot 1 \cdot 10 W = 5880 J$

b. La escalera ahora está inclinada formando un ángulo de $30 °$ respecto a la vertical, por lo que sólo la componente vertical del peso será la que producirá trabajo.

Datos:
$F = p e s o = 588 N$
$∆ \vec{x} = 10 m$
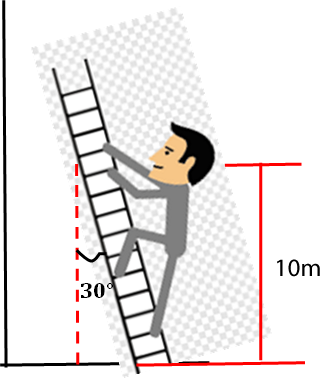$α = 0 °$ respecto a la dirección del movimiento (vertical) (El peso no está inclinado, solo la escalera)

Sustituyendo los datos en la ecuación que define el trabajo:

$W = F \cdot \cos α \cdot ∆ \vec{x} W = 588 \cdot 10 W = 588 \cdot 10 W = 5 880 J$

5. Dos personas jalan una caja para regalarle a su mamá un gran oso de peluche. Cuando comienzan a mover la caja, no se han puesto de acuerdo donde guardar el regalo. Arturo inicia jalando hacia la cochera, con una fuerza de $250 N$ , mientras que su hermana, Susana jala al mismo tiempo otra cuerda hacia el jardín, para esconderla en un almacén que tienen allí. Ella utiliza una fuerza de $120 N$ . La caja se desplaza $3 m e t r o s$ , en la dirección en la que Arturo está jalando. ¿Cuál es el trabajo resultante sobre la caja con el oso de peluche?

Datos:

$\vec{F_{1}} = - 250 N \vec{F_{2}} = + 120 N ∆ \vec{x} = - 3 m$

La fuerza que va a actuar sobre la caja es la resultante entre las fuerzas que Arturo y Susana aplican jalando la caja. Por ello aplicamos la fórmula:

${\vec{F}}_{r} = {\vec{F}}_{1} + {\vec{F}}_{2}$

Sustituyendo los valores de dichas fuerzas, tenemos:

$\vec{F_{r}} = \vec{F_{1}} + {\vec{F}}_{2} = - 250 + 120 = - 130 N$ fuerza resultante que actúa sobre el cuerpo y ocasionará el desplazamiento hacia Arturo (signo negativo, porque su sentido es hacia la izquierda)

Ahora, como la fuerza resultante es paralela a la dirección del desplazamiento y por consecuencia, el ángulo entre la fuerza y el desplazamiento es igual a cero, podemos emplear la fórmula:

$W = {\vec{F}}_{r} \cdot ∆ \vec{x}$

Y sustituyendo la fuerza resultante y el desplazamiento, se obtiene:

$W = {\vec{F}}_{r} \cdot ∆ \vec{x} = - 130 \cdot (- 3) = 390 J$

El trabajo total realizado es 390 Joules.

6. El siguiente gráfico representa la fuerza de $10 N e w t o n s$ , ejercida sobre un resorte. ¿Qué trabajo efectúa la fuerza al estirarlo desde $x_{i} = 2 c m$ hasta $x_{f} = 7 c m$ ?

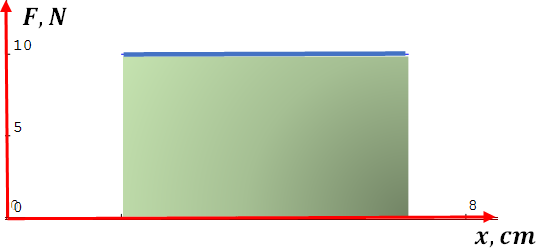
Datos:
$F = 10 N$
$∆ \vec{x} = 7 - 2 = 5 c m \cdot \frac{1 m}{100 c m} = 0, 05 m$ cuidado, hay que transformar a metros el desplazamiento

El área del rectángulo debajo de la línea fuerza-desplazamiento es el trabajo realizado, de tal manera calcularemos dicha área, como el área de cualquier rectángulo.

$A = b a s e \cdot a l t u r a$

$W = 0, 05 \cdot 10 = 0, 5 J$

El trabajo realizado para alargar el resorte desde $2 c m$ hasta $7 c m$ fue $0, 05 J$ .

7. ¿A qué altura se debe encontrar una silla de $5 k g$ para que en su caída desarrolle un trabajo de $90 J$ ?

Datos:

∆ \vec{x} = ?

$W = 90 J$

$m = 5 K g$

Dado que la fuerza que ocasiona que la silla caiga es la fuerza de la gravedad, o sea el peso de la silla,

\vec{F} = m \cdot \vec{g}

y dado que

1- Temperatura

En el lenguaje común usamos la palabra “calor” para referirnos a una sensación opuesta al frío; así pues, confundimos el calor con la temperatura.

La temperatura es una propiedad de la materia, mientras que el calor expresa una transferencia de energía.
La temperatura es la medida del grado de agitación térmica que tienen las partículas que componen un cuerpo. Ese movimiento produce la dilatación y los cambios de estado.

2- Calor

Es una de las manifestaciones de la energía. El calor se debe a la energía cinética de las moléculas del cuerpo y ésta función (depende) de la temperatura.

El calor es un proceso en el que la energía térmica se transfiere de un cuerpo caliente a otro más frío. Se suele llamar cantidad de calor a la cantidad de energía así transferida.

Los principales efectos del calor son:

a) Aumentar la temperatura de los cuerpos.

b) Dilataciones de los cuerpos; es decir, puede producir variaciones de longitud, de superficie y de volumen de los cuerpos.

c) Cambio de estado, ej. el hielo mediante el calor puede transformarse en agua y ésta en vapor.

d) Cambio de color. Ej. fierro al rojo.

e) Deformaciones de los cuerpos Ej. La cera cambia fácilmente de forma al calentarlos.

f) Efectos químicos. Hay muchas sustancias que se descomponen al calentarlas.

g) Efectos fisiológicos, Ej. La insolación, quemaduras de la piel, etc.

h) Efectos termoeléctricos. Se construyen pilas eléctricas aprovechando el llamado efecto Seebeck que se estudia en termoelectricidad.

i) Produce también variaciones en la resistencia eléctrica de los cuerpos.

j) Variaciones en la tensión de los gases y vapores.

k) Destruye la imanación de los cuerpos, Ej. Las tijeras y cuchillos imantados basta calentarlos para desimantarlos.

3- Escalas Termométricas

Para poder comparar el estado calórico de los cuerpos y poder decir si un cuerpo está más frío o caliente que otro, es necesario tener algunos puntos de referencia. Esto se consigue con los termómetros que miden la temperatura de los cuerpos y pueden graduarse de diferentes maneras.

El termómetro más conocido es el líquido (mercurio o alcohol coloreado) que se compones de un tubo capilar ensanchado en su extremo inferior o bulbo; una vez introducido el líquido, se cierra el tubo (algunas veces se cierra al vacío). Al subir la temperatura aumentará el volumen del bulbo del tubo capilar y del líquido, pero como éste se dilata más que el material del tubo, el líquido ascenderá por el capilar al producirse un calentamiento o descenderá por un enfriamiento.

Se obtienen así distintas escalas termométricas, siendo tres las más usadas:

1° La escala Celsius o centígrada, cuyos grados se abrevian " °C o t°_c".
Asigna el valor 0°C (cero grados Celsius) al punto de fusión del hielo y 100°C al punto de ebullición del agua. Este intervalo divide en 100 partes iguales el tubo capilar, constituyendo cada una de ellas 1°C. La división se continúa sobre el °100 para temperaturas superiores y bajo el 0° para temperaturas inferiores o negativas.

2° La escala Fahrenheit, de uso en los países anglosajones, cuyos grados se abrevian " °F o t° _F ".
Asigna el valor de 32°F (32 grados Fahrenheit) al punto de congelación del agua y 212°F para los vapores de agua hirviendo a 1at de presión. El espacio entre 32°F y 212°F se divide en 180 partes iguales constituyendo cada una de ellas 1°F.

De lo anterior se deduce que al intervalo de 100°C corresponden 180°F, de donde:

1°C = 9/5 °F y 1°F = 5/9 °C

Estos factores de conversión permiten expresar una temperatura en °C en su equivalente °F. Pero para esto es más fácil determinar una fórmula que relacione ambas escalas:

grados_fahrenheit.jpg (210×104)

3° Escala absoluta o de Kelvin cuyos grados se abrevian " °T o °K ".

En esta escala, 273 K corresponden a la temperatura en que el agua se congela, y 373 K, a la temperatura de ebullición del agua. Esta escala posee 100 divisiones entre estos valores.

Asigna el valor 0°K (cero kelvin) a la temperatura que llamamos cero absoluto, que corresponde a una temperatura de -273 °C; en termodinámica se verá que el 0°K = -273°C es la temperatura más baja que puede existir. por lo tanto no existen temperaturas negativas en la escala absoluta. Como los °C y los absolutos son del mismo tamaño y estando el 0°K "corrido" 273° más abajo que el 0°C, bastará con sumar 273° a los °C para expresarlos en absolutos o Kelvin.

Luego podemos escribir relaciones:

T° = t°_c + 273 y t°_c = T° – 273

Ejercicios:

1- La temperatura normal del cuerpo humano es 37°C ¿Cuánto es en grados Fahrenheit?

t_c = 37°

t_f = x

grados_fahrenheit.jpg (210×104)

Luego:

37 = 5
x-32 9

5 • ( x – 32) = 37 • 9

de donde :

x = 98, 6 °F

2- La temperatura máxima de ayer en New York fue 77°F¿Acuánto corresponde en °C y en grados absolutos?

tf = 77°

tc = x₁

T = x₂

grados_fahrenheit.jpg (210×104)

x = 5
77 – 32 9

Donde:

9x = 5 • 45

t_c = 25°C

Ahora calculamos los grados absolutos:

T = t_c + 273

T = 25 + 273

T = 298°K

3- ¿A qué temperatura un termómetro centígrado marca lo mismo que y un termómetro fahrenheit?

t_c = x

t_f = x

x = 5
x- 32 9

9x = 5x – 160

de donde:

x = -40

es decir: -40 °C = -40°F

4- Tipos o clases de termómetros

La propiedad que más se usa en la construcción de termómetros es la dilatación que experimentan los cuerpos por el calor; basado en esto se construyen termómetros sólidos (termómetros metálicos), líquidos (los más corrientes son de mercurio o de alcohol) y de gases (termómetros de aire y de hidrógeno). Pero sin duda los de uso más común son los de mercurio introducido al vacío en un tubo de vidrio. En esta forma se puede medir temperaturas entre -39°C, que es el punto de solidificación del mercurio, y 300°C que es el punto de ebullición al vacío.

Sin embargo, se construyen termómetros de Hg (mercurio) que pueden medir temperaturas sobre 500° pero para ello se sustituye el tubo de vidrio por uno de cuarzo y se introduce nitrógeno a gran presión sobre el Hg del capilar.

3.1 Termómetro Líquido

El mercurio es estimado universalmente como el líquido termométrico por excelencia, debido a las siguientes características:

– Sus puntos límites bastante separados (-39°C y 357 °C a presión normal) determinan un amplio margen de temperaturas medibles suficientes para los usos más corrientes.

– Su dilatación es bastante regular, lo que favorece la precisión del instrumento.

– Posee una baja capacidad calórica, por lo que basta una pequeña cantidad de calor para que su temperatura se eleve en forma rápida y apreciable, dando gran sensibilidad al instrumento.

– Es fácil de obtener químicamente puro.

– No moja el vidrio, por lo cual no influye la capilaridad del tubo. El termómetro médico o clínico de mercurio sólo puede medir temperaturas máximas. Esto se debe a que presenta en la salida del bulbo una pequeña estrangulación que hace que el mercurio pueda subir por el capilar pero no regresar, por lo que se requiere agitarlo para que el líquido baje.

Dentro de los termómetros líquidos, podemos encontrar:

a- Termómetro clínico: Es el termómetro que el médico usa para tomar la temperatura de un enfermo. Cerca del bulbo tiene una estrangulación, que no impide que el mercurio pase por ella cuando la temperatura sube. Pero cuando la temperatura baja, el mercurio no puede pasar del bulbo, quedando registrada la máxima temperatura alcanzada. Sacudiendo el termómetro se consigue que el mercurio vuelva al bulbo.

termometro.jpg (218×219)

b- Termómetro de máxima y mínima: Sirve para determinar cuál ha sido la mayor temperatura en un determinado lapso, por ejemplo, en un día. Se lo emplea en las estaciones meteorológicas.

Tiene forma de U y en su interior lleva dos líquidos: mercurio y alcohol. Además en su interior lleva un índice de acero en cada rama que permite dejar indicada la máxima y la mínima temperatura alcanzada en cierto lapso. Se gradúa con la ayuda de un baño térmico controlado por un termómetro patrón. La rama superior del lado izquierdo está lleno de alcohol y la del lado derecho tiene alcohol hasta cierto nivel, dejando un espacio libre para las posibles dilataciones.

Al producirse una variación de la temperatura se producirán dilataciones o contracciones de los líquidos de acuerdo con ella lo que producirá el arrastre de los índices correspondientes por el mercurio. En esta forma la parte inferior del índice de la derecha dejará indicada la Máxima temperatura alcanzada y la parte inferior del índice de la izquierda indicará la Mínima.

Para poner nuevamente en contacto dichos índices con el mercurio se hace uso de un pequeño imán. La temperatura que existe en el momento de la observación se lee en el nivel de la columna de HG en cualquiera de las ramas.

3.2- Termómetro Sólido

Están construidos sobre la base de dos materiales que presentan un coeficiente de dilatación muy distinto.

termometro_solido.jpg (754×489)

Las figuras 3 y 4 ilustran dos variantes de este tipo de termómetro. En el primer caso la varilla posee un gran coeficiente de dilatación respecto del soporte, ya que al incrementarse la temperatura del dispositivo y alargarse más la varilla que el soporte, la aguja se mueve. En el segundo caso se trata de dos varillas con distinto coeficiente de dilatación, soldadas a lo largo. Al aumentar la temperatura, la varilla con mayor coeficiente de dilatación se estira más que la otra y el conjunto se curva.

Entre estos, podemos encontrar:

a- – Termómetro metálico: El calentamiento hace que un espiral bimetálico calibrado previamente se curve, moviendo la aguja que señala el valor de la temperatura.

b- – Termómetros de termopar: De uso frecuente en las industrias para registros continuos y control de temperatura. Se basan en la medida del voltaje existente en las uniones de cables metálicos o conexiones de naturaleza diferentes, la que depende de las temperaturas de las uniones.

3.3.- Termómetro gaseoso

Este termómetro (también denominado termoscopio), inventado por Galileo Galilei, emplea aire (o cualquier gas) como elemento termométrico,

3.4- Otros termómetros

a- Pirómetro óptico: La temperatura de un objeto (como horno, metal fundido) se obtiene comparando el color de la llama con el del filamento de una lámpara eléctrica.

b- Termómetro de resistencia eléctrica: Algunos termómetros de este tipo usan semiconductores (por ejemplo, germanio). Son los más recomendados para medir temperaturas muy bajas (entre 0,2K y 50K).

c- Termómetros magnéticos: Se sustentan en la medición de las propiedades magnéticas de determinados materiales que varían con la temperatura. Se los utiliza para medir temperaturas menores de 1 Kelvin (1K).

d- Termómetros acústicos: El principio en que sustenta el funcionamiento de estos aparatos es una variación de la velocidad del sonido (o de ultrasonido), de acuerdo con la temperatura. Se utilizan para temperaturas bajas (2K a 40K).

Comparte este contenido:

Todo el contenido y material en este sitio es propiedad de Wited y está protegido por derechos de autor.

La reproducción, distribución o uso sin permiso está prohibida y es ilegal. Se permite la referencia sin uso comercial solo con atribución adecuada y enlace a la fuente original.

Fecha de publicación: 06/03/2024

Última edición: 06/04/2024

Estudia

Practica

Pregunta

Trabajo y potencia

Te recomendamos seguir estudiando estos temas

Círculo y circunferencia: área, perímetro y longitud

Dramatizar

Elementos secundarios del triángulo: simetrales y transversales de gravedad

Trimestral

USD $46 /3 meses

Estudia

Practica

Pregunta

Trabajo y potencia

Te recomendamos seguir estudiando estos temas

Círculo y circunferencia: área, perímetro y longitud

Dramatizar

Elementos secundarios del triángulo: simetrales y transversales de gravedad

Contáctate con nuestro equipo comercial

No tienes acceso a este recurso

Resuelve tus dudas con los profesores de Wited

Escribe tu pregunta

Trimestral

USD $46 /3 meses