Tabla de doble entrada

1- Tabla de doble entrada

Una tabla de doble entrada o también denominada tabla de contingencia, es aquella en la que se quiere estudiar dos variables para una misma muestra. 

Esta tabla se utiliza cuando queremos estudiar una muestra o población, pero bajo dos características o variables.

Para poder realizar estas tablas, debemos:

1. Determinar cuáles son las variables que se quieren estudiar
 

2. Determinar los intervalos para cada una de estas variables. 
 

3. Llenar las tablas con los datos recolectados.

En estas tablas se utilizan solo los intervalos y las frecuencias absolutas de cada intervalo.

Las frecuencias acumuladas y las relativas se utilizan solamente en las tablas de frecuencias simples.

Se puede decir que las tablas de contingencia es la mezcla de dos tablas de frecuencias, ya que se estudian dos variables para una misma muestra.

Estas tablas tienen columnas y filas, ya que una de las variables se registra en columnas y la otra variable se registran en filas. El cruce de estas columnas y filas es lo que genera la doble entrada en las tablas de contingencia.

 

Ejemplo 1:

 

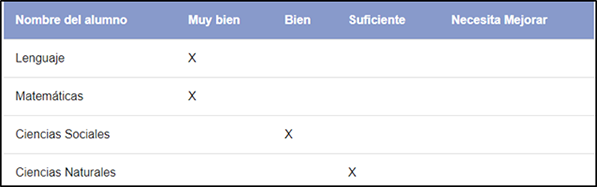
Como se visualiza en la imagen, se realiza un estudio sobre el desempeño de un alumno en diversas asignaturas, en este caso las variables a estudiar son: desempeño y Asignaturas.

Como se visualiza una de las variables se sitúa en las columnas y la otra variable se sitúa en las filas, las frecuencias se van llenando según la información obtenida. 

 

Ejemplo 2:
En una encuesta se recogieron los datos de 10 sujetos respecto al estado civil y el sexo de cada uno.
Los resultados fueron los siguientes:

 
hombre casado;hombre soltero;mujer soltera;mujer divorciada;hombre casado; 
hombre divorciado;mujer soltera;hombre soltero;mujer casada;hombre divorciado.

1- Realice la tabla de doble entrada correspondiente al estudio.

Solución: 

Para poder dibujar la tabla de doble entrada debemos primero determinar ¿Cuáles son las variables que se van a estudiar?

En este caso se van a estudiar las variables estado civil y sexo.

Luego debemos determinar que variable estará en las columnas y cual en las filas. En este caso nos quedaría:

 

Estado civil
Sexo

    

Una vez hecho esto, tenemos que determinar los intervalos o las posibles respuestas que nos pueden dar: 
 

Para el caso del estado civil, las posibilidades son: Casada(o), Soltera(o), Viuda(o), Divorciada(o).

Para el caso del sexo las posibilidades son:

Hombre, mujer.

Llenando la tabla nos queda:

 

Estado civil	C	S	D	V
Sexo
H
M

     

Una vez dibujada la tabla de contingencia debemos llenar con la información obtenida, es decir,

Como la primera persona es hombre y casado, debemos situarnos en la celda donde se cruza el estado civil casado con la sexualidad hombre quedando así:

 

Estado civil	C	S	D	V
Sexo
H	1
M

  

Colocamos un 1, ya que es una persona que cumple esas características, llenando la tabla con las 10 personas nos quedaría:

 

Estado civil	C	S	D	V
Sexo
H	1+1	1+1	1+1
M	1	1+1	1

 

 

Al realizar las sumas correspondientes nos queda:

 

Estado civil	C	S	D	V
Sexo
H	2	2	2
M	1	2	1

Ahora solo nos queda hacer la suma de cada una de las categorías. 

 

Estado civil	C	S	D	V	Total
Sexo
H	2	2	2	0	6
M	1	2	1	0	4
Total	3	4	3	0	10

 

Una vez completada la tabla podemos calcular porcentajes y probabilidades, como también deducir conclusiones.

Si quisiéramos saber ¿Cuál es la probabilidad de sacar una persona al azar y que sea hombre? 

Solo aplicamos Laplace y nos quedaría:

$P(H)=\frac{6}{10}\to \mathrm{0,6}$

Como también podemos deducir que la mayoría de las personas encuestadas son hombres o que ninguna mujer encuestada es viuda. 

Y así podemos obtener varias conclusiones.

 

Ejemplo 3:
Se quiere realizar un experimento sobre el género y la edad de 10 estudiantes de un colegio que participan en las olimpiadas de matemáticas. Se recogieron los siguientes datos:

hombre 18 años;hombre 25 años;mujer 18 años;mujer 20 años;hombre 21 años;
hombre 21 años;mujer 23 años;hombre 25 años;mujer 23 años;hombre 20 años

a- Realice la tabla de doble entrada correspondiente al experimento
b ¿Qué porcentaje de participantes son hombres?

Solución: 

 Primero determinaremos las variables que se estudian en el experimento, en este caso son:

– Género de estudiantes.
– Edad de estudiantes.

Ahora vamos a determinar los intervalos o categorías para cada una de las variables.

En el caso del género solo podemos tener dos categorías

– Hombre
– Mujer

En el caso de las edades es recomendable crear intervalos ya que hay mucha diferencia entre la edad del estudiante mayor y el menor.

Utilizaremos intervalos de amplitud 3. Quedando los siguientes intervalos:

– [18,21)
– [21,24)
– [24,27)

Recordar que la amplitud de intervalo puede ser cualquiera, ya que uno elige la amplitud que desea, nosotros elegimos una amplitud de 3, para poder tener pocos intervalos. 
 

Si se desea elegir cada edad como un intervalo, también es válido, solo que para este caso nos quedarían 7 intervalos.

Al dibujar la tabla nos quedaría:

 

Edad de estudiantes	[18,21)	[21,24)	[24,27)	Total
Género
H
M
Total

          

Continuaremos con llenar los datos recogidos quedando la tabla de la siguiente forma:

 

Edad de estudiantes	[18,21)	[21,24)	[24,27)	Total
Género
H	1+1	1+1	1+1
M	1+1	1+1
Total

 

Al hacer las sumas correspondientes nos queda:

Edad de estudiantes	[18,21)	[21,24)	[24,27)	Total
Género
H	2	2	2	6
M	2	2		4
Total	4	4	2	10

 

Una vez completada la tabla, responderemos la siguiente pregunta:

b- ¿Qué porcentaje de participantes son hombres?
 

Para determinar el porcentaje de estudiantes hombres que participan, solo debemos aplicar la regla de 3 simple para porcentajes.

$$\begin{gathered} 100\%\to 10 \\ X\%\to 6 \end{gathered}$$

Aplicando la regla de tres simples nos queda:

 

 

$$\begin{gathered} 100·6 = 10·x \\ \frac{100·6}{10}= x \\ \mathbf{60}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{x} \end{gathered}$$

 

Entonces el porcentaje de hombres que participan es del 60%

 

Ejemplo 4:

En una clase de 32 estudiantes se pregunta que prefieren jugar, un partido de futbol o uno de baloncesto. De los chicos hay 15 que prefieren el futbol y 4 que prefieren el baloncesto de las chicas 10 el Fútbol y 3 el baloncesto.

a- Realice la tabla de doble entrada.
b- ¿Cuál es el porcentaje de estudiantes que prefieren baloncesto?

Solución:

a- Para poder realizar la tabla de doble entrada, debemos determinar las variables que se van a estudiar. En este caso son:

– Género
– Deporte

Y la categorización de cada uno es la siguiente:

– Género: Niño y Niña
– Deporte: Baloncesto y Futbol.

Al dibujar la tabla de doble entrada nos queda:

Género	Niño	Niña	Total
Deporte
Futbol
Baloncesto
Total

 

Ahora tabularemos los datos que entrega el ejercicio, quedando la completada la tabla:

 

Género	Niño	Niña	Total
Deporte
Futbol	15	10	25
Baloncesto	4	3	7
Total	19	13	32

 

Una vez completada la tabla, responderemos la pregunta:

¿Cuál es el porcentaje de estudiantes que prefieren baloncesto?
Como nos pide el porcentaje de estudiantes que prefieren baloncesto, pero no especifica si debe ser niño o niña, entonces asumimos que se debe tomar el total de estudiantes que prefieren baloncesto sin importar si son niños o niñas los que lo prefieran. Aplicando la regla de tres simples nos queda:
 

 

$$\begin{gathered} 100\% \to 32 \\ x \%\to \; \; 7 \end{gathered}$$

 

Aplicando multiplicación cruzada nos queda:

 

$$\begin{gathered} 100·\mathrm{7=32}·x \\ 700 = 32x \\ \frac{700}{32}=x \\ \mathbf{21}\mathbf{,88\%}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{x} \end{gathered}$$

 

Entonces el porcentaje de estudiantes que prefieren baloncesto es del 21,88%