1.- Sistema de ecuaciones lineales
Un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones de primer grado, en el cual se relacionan dos o más incógnitas.
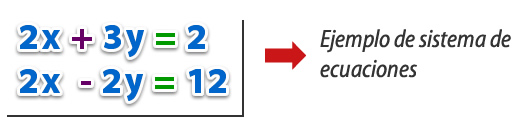
En los sistemas de ecuaciones, se debe buscar los valores de las incógnitas, con los cuales al reemplazar, deben dar la solución planteada en ambas ecuaciones.
A cada una de las ecuaciones se les denomina también restricciones o condiciones.
Todo sistema de ecuaciones lineales con dos incógnitas, x e y, tiene las siguientes representaciones:
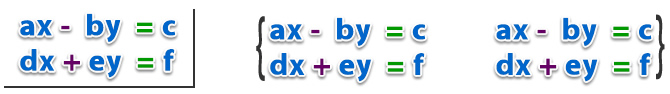
Donde x e y son las incógnitas, y a,b,c,d,e y f son coeficientes reales (ℝ).
Las incógnitas establecidas en un sistema representan el punto donde se intersectan las rectas en un plano cartesiano (x,y).
1.1- ¿Qué es un plano cartesiano?
Por si no lo recuerdas, un plano cartesiano son 2 rectas numéricas perpendiculares, una horizontal y otro vertical que se cortan en un punto llamado origen o cero del sistema.
2- Métodos de resolución algebraica para sistemas de ecuaciones
a) Reducción
Consiste en igualar los coeficientes de una misma incógnita en ambas ecuaciones y, enseguida, sumar o restar las ecuaciones, de modo que se eliminen los términos cuyos coeficientes se igualaron.
Ejemplo:
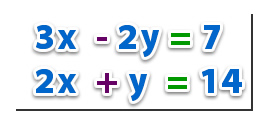
Paso 1- Igualaremos una de las incógnitas del sistema. En este caso, nosotros empezaremos igualando la incógnita y. Para ello, multiplico la segunda ecuación por 2, quedando 4x+2y= 28

Paso 2- Ahora, sumamos o restamos (según se requiera) los términos semejantes, para reducir (eliminar) el término con coeficiente común.

Luego, resuelvo la ecuación, quedando así x=5, ya que:
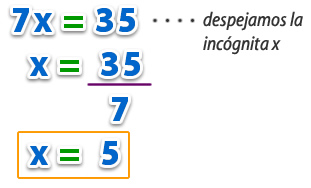
Ya tenemos el valor de una de las incógnitas. Para identificar el otro valor, debemos remplazar en una de las ecuaciones el valor que obtuvimos de x. en este caso:

Por lo tanto la solución a nuestro sistema de ecuaciones es → S: (5, 4)
b) Sustitución
Consiste en despejar una incógnita de una de las ecuaciones y sustituirla en otra ecuación.
Ejemplo:
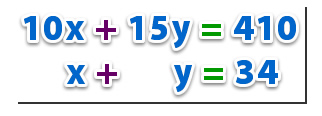
Primero, despejaremos cualquiera de las incógnitas de esta ecuación. Nosotros escogeremos despejar x en la segunda ecuación. Para ello, moveremos todos los términos que no sean x hacia el otro lado de la igualdad.

Conociendo el valor de x, sustituimos en la otra ecuación:
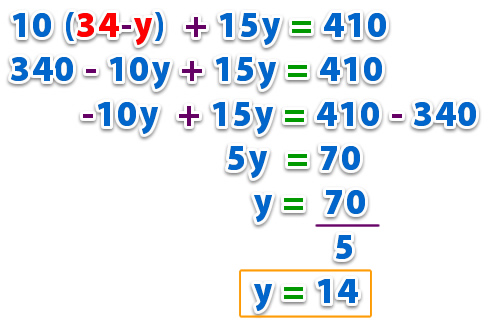
Una vez conocemos el valor de la otra incógnita (en este caso, y), sustituimos en la ecuación:
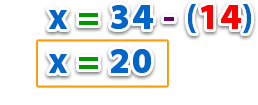
Solución: (20,14)
c) Igualación
Consiste en despejar la misma variable de ambas ecuaciones del sistema. Una vez despejada, se igualan los resultados, despejando la única variable que queda.
Ejemplo:
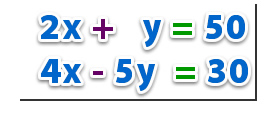
1°Debemos despejar cualquiera de las incógnitas de la ecuación. En este caso, nosotros optamos por despejar y.
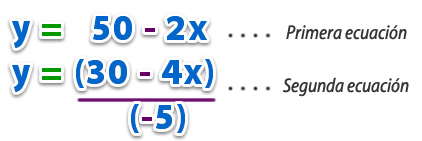
2° Se igualan las expresione obtenidas: y = y
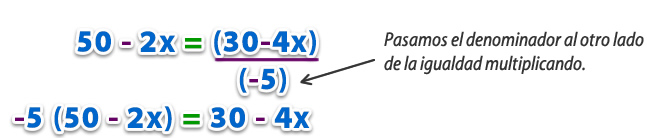
3° Ahora, se resuelve la ecuación resultante, que tiene una incógnita:

Una vez identificado el valor de «x», remplazamos en cualquiera de las ecuaciones del sistema.
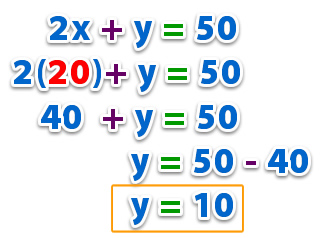
Solución: (20,10)
3- Tipos de sistemas
Existen 3 tipos de sistemas de ecuaciones: Los sistemas equivalentes, los sistemas sin solución o incompatibles, y los sistemas con infinitas soluciones o compatible indeterminado.
a- Sistemas equivalentes
Son aquellos que se caracterizan por tener una única solucióna partir de dos incógnitas. En el plano cartesiano, se representan al formarse rectas secantes (solo un punto en la recta).
Por ejemplo:
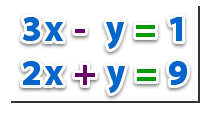
Realizando las operaciones de suma y resta, se obtiene:
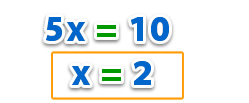
Remplazando:
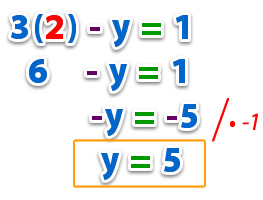
S (2,5)
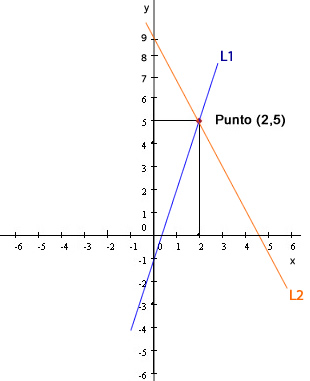
b– Sistema incompatible:
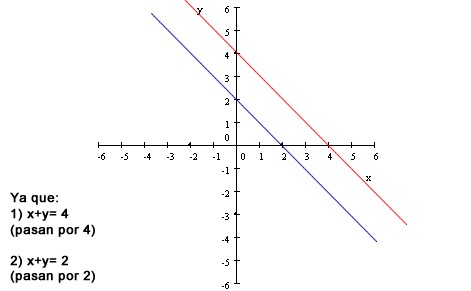
Son aquellos sistemas en donde no hay ninguna solución posible. En el plano cartesiano, se representan con rectas paralelas (ningún punto).
Ejemplo:
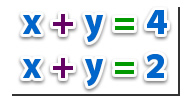
En el ejemplo anterior, podemos observar que dos ecuaciones iguales dan como resultado un número distinto. Esto quiere decir que las ecuaciones no tienen resultados en común, ya que si los tuviese, el resultado de ambas ecuaciones sería el mismo.
En el plano cartesiano, las ecuaciones se representarían de una forma independiente. Se obtienen dos rectas paralelas (no se intersecan). Por lo tanto, el sistema no tiene solución.
c- Sistemas compatible indeterminado:
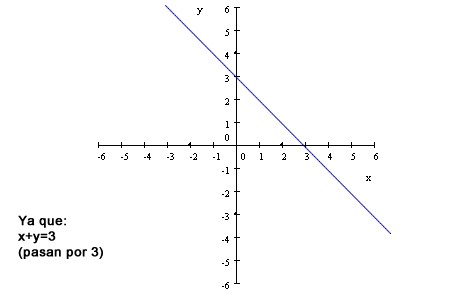
Son aquellos sistemas en donde existen infinitas soluciones. En el plano cartesiano, se representa con rectas coincidentes (infinitos puntos).
Ejemplo:

En este caso, podemos observar que las ecuaciones de este sistema son exactamente iguales, ya que 2x+2y=6 es lo mismo que x+y=3, pero amplificado por 2. Esto quiere decir, que cualquier punto de la recta es la solución del sistema.
Por lo tanto:
3.1- ¿Cómo identificar cada sistema?
Identificar un sistema es muy sencillo. Para hacerlo, debes tener en cuenta las siguientes consideraciones:
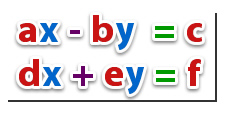
– Si la multiplicación entre a y e, y la multiplicación entre b y d dan valores distintos, significa que el sistema es equivalente.
– Si la multiplicación entre a y e, y la multiplicación entre b y d dan valores iguales, significa que el sistema o es incompatible, o es un sistema compatible indeterminado. Para identificarlo, debemos tener en cuenta las siguientes consideraciones:
a) Si la multiplicación entre b y f, y la multiplicación entre c y e dan valores distintos, significa que el sistema es incompatible.
b) Si la multiplicación entre b y f, y la multiplicación entre c y e dan valores iguales, significa que el sistema es compatible indeterminado.
4- Resolución de problemas con sistemas de ecuaciones
Para resolver problemas en los que se plantee un sistema de ecuaciones, debemos seguir estos pasos:
1.º Leer atentamente el enunciado, e identificar las incógnitas.
2.º Traducir el enunciado en varias ecuaciones.
3.º Resolver el sistema e interpretar la solución.
Ejemplo:
La suma de la edad de dos niños es 4 años. Si la edad del primero sumada al triple de la edad del segundo es 10 años. ¿Qué edad tiene cada niño?
Pasos:
1.º Leer atentamente el enunciado, e identificar las incógnitas.→ Números pedidos, x e y
2.º Traducir el enunciado en varias ecuaciones.
La suma de la edad de dos niños es 4 años → x + y = 4
la edad del primero sumada al triple de la edad del segundo es 10 años → x + 3y = 10
3.º Resolver el sistema e interpretar la solución.
x+y = 4
x+3y = 10
Utilizamos el método de reducción
Respuesta: Las edades son : 1 y 3 años

