1- Reducción de términos semejantes
Como has visto en las clases anteriores el lenguaje algebraico expresa el lenguaje natural mediante el uso de letras y números.
Las expresiones algebraicas representan generalizaciones que facilitan los cálculos. Por ejemplo, para determinar el área y el perímetro de un cuadrado solo se debe conocer cuánto mide el lado para realizar los cálculos ya que existe una regla general para esos casos.
Observa la siguiente situación:
1- Laura tiene una colección de 3 bolitas azules y 4 verdes, mientras que su hermano Camilo tiene 2 bolitas azules y 3 verdes. ¿Cuántas bolitas de cada color tienen entre los dos?

Para representar la situación mediante una expresión algebraica se puede denotar con una letra. Para referirse a las bolitas verdes se utilizará V y para las azules se nombrará con la letra A respectivamente.
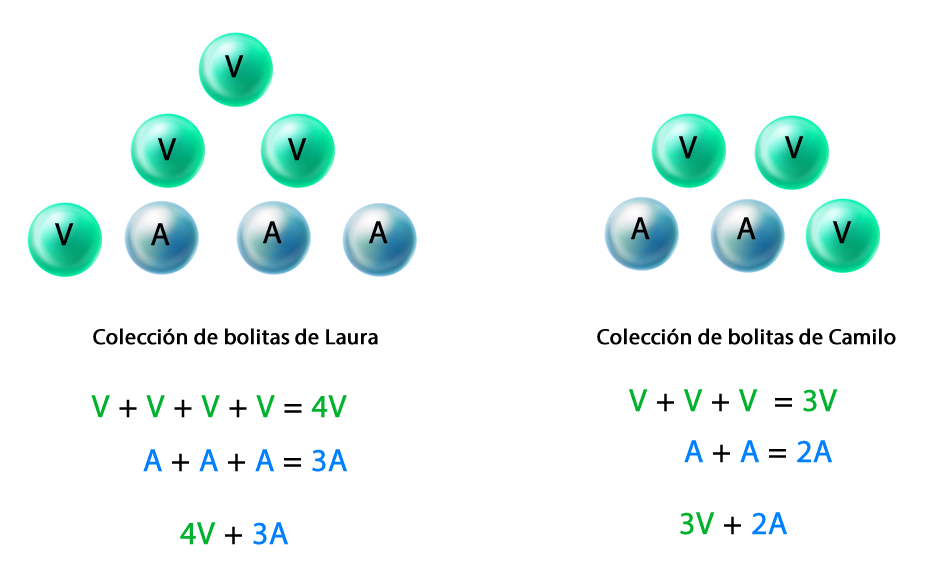
Entonces, para conocer las bolitas de cada color que tienen entre los dos se juntan los términos que tengan el mismo factor literal, es decir, que tengan las mismas letras.
Luego, se realiza una adición entre los términos que tienen el mismo factor literal. Se suman los números, mientras que las letras se dejan expresadas.
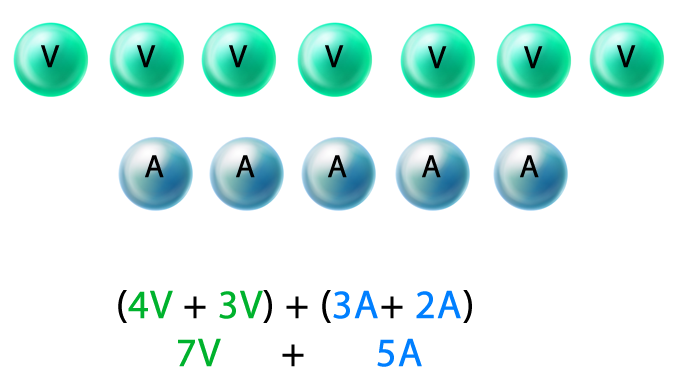
Finalmente, se puede establecer que entre los dos hermanos tienen 7 bolitas verdes y 5 azules que algebraicamente se puede expresar como 7V + 5A.
2- Si Laura le da 2 bolitas verdes y una azul a su hermano Camilo. ¿Con cuántas bolitas de cada color queda Laura?
Primero, se representa la cantidad las bolitas que tiene Laura:
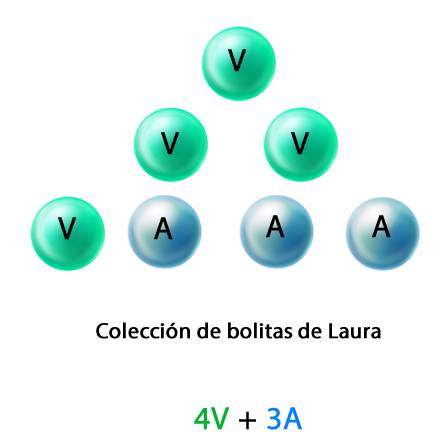
Luego, se expresa la cantidad de bolitas menos que tendrá tachando la cantidad que le regalará a su hermano.
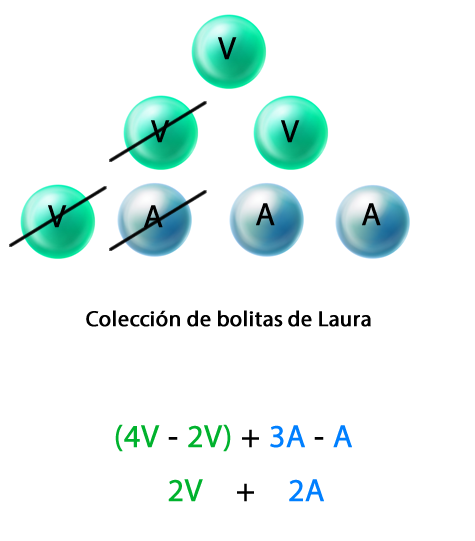
De acuerdo con la representación, Laura quedará con 2 bolitas verdes y 2 azules.
Entonces, ¿qué son los términos semejantes y cómo se pueden reducir?
Se llaman términos semejantes a todos aquellos términos que tienen igual factor literal, es decir, a aquellos términos que tienen iguales letras (símbolos literales) e iguales exponentes.
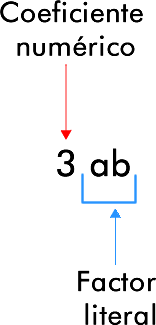
Ejemplo: 2mn y -8mn son términos semejantes
Reducir términos semejantes significa sumar o restar los coeficientes numéricos en una expresión algebraica, que tengan el mismo factor literal.
Para desarrollar un ejercicio de este tipo, se suman o restan los coeficientes numéricos y se conserva el factor literal.
– Para reducir términos semejantes con el mismo signo, se suman los coeficientes de todos los términos y se antepone, al coeficiente total, el mismo signo que comparten, y a continuación se escribe la parte literal.
Ejemplo:
x + 4x = 5 x
11b + 9 b = 20b
– Para reducir dos términos semejantes de distinto signo, se halla la diferencia entre los coeficientes de los términos,colocando antes de esta diferencia el signo del coeficiente mayor (en valor absoluto) y a continuación
se escribe la parte literal.
Ejemplo:
15m – 5m = 10 m
-30x + 12x = -18x
Nota: dos términos semejantes con igual coeficiente y distinto signo se anulan.
1.1- Reducción de un polinomio que contenga términos semejantes de diversas clases
Para reducir un polinomio con diversos términos semejantes de diversas clases, se procede de la siguiente manera:
1- Se agrupan los términos semejantes de cada clase en un mismo paréntesis.
2- Se reducen los términos semejantes.
3- Se da la respuesta, ordenando el polinomio resultante.
Nota:
Recordemos que los términos semejantes son aquellos que tienen las mismas letras y afectadas por los mismos exponentes.
Ejemplos:
a) -81x + 19y – 30z + 6y + 80x + x – 25y
Agrupamos los términos semejantes:
(-81x + 80x + x ) + (19y+ 6y –25y) – 30z
Reducimos términos semejantes (sumamos o restamos) y damos la respuesta.
-30z
b) -6m + 8n +5 –m –n -6m -11
1° Se agrupan términos semejantes
(-6m –m -6m) + ( 8n –n) + (5 – 11)
2° Reducimos términos semejantes (sumamos o restamos)
(-13m) + (7n) + (-6)
3°Se da la respuesta, ordenando el polinomio resultante.
-13m + 7n – 6
¿Cómo expresarías de manera algebraica el perímetro de las siguientes figuras geométricas?
a.
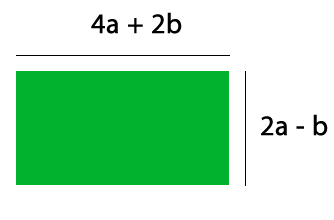
El perímetro es la suma de todos los lados, en el caso del rectángulo tiene dos pares de lados que tienen la misma medida, lo que se puede expresar de la siguiente manera:
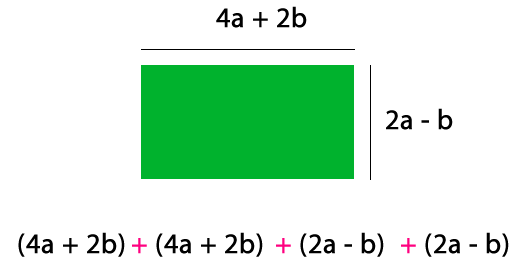
Destacas con el mismo color las expresiones que tienen el mismo factor literal y los agrupas.
(4a + 4a + 2a + 2a) + (2b + 2b – b – b)
12a + 2b
b.
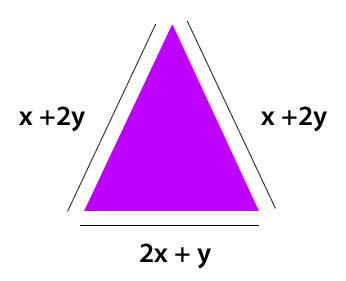
En la imagen se aprecia un triángulo isósceles, ya que posee dos lados de la misma medida y el lado restante mide distinto.
Al igual que en el caso del rectángulo, las medidas de sus lados se escriben como sumandos y se agrupan los términos que tienen los mismos factores literales para reducir la expresión.
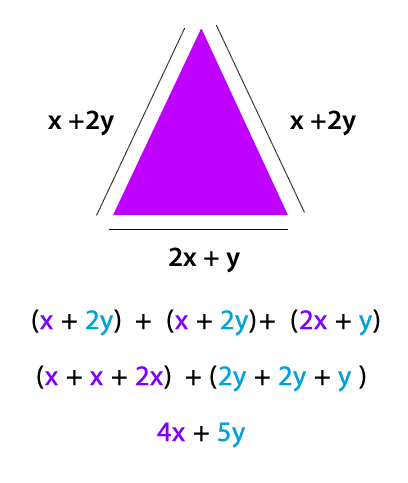
1.2- Términos entre paréntesis
Los paréntesis más usados son:
{ } = Llaves
[ ] = Corchetes
( ) = Redondos
Si encuentras ejercicios donde se presentan paréntesis dentro de otro paréntesis, estas expresiones se resuelven de adentro hacia fuera.
Al reducir términos semejantes que estén expresados entre paréntesis se debe considerar lo siguiente:
⇒ Si un paréntesis es precedido por un signo (+) este se suprime sin variar los signos de los términos que están dentro del paréntesis.
Ejemplo:
7a + (-3a + 5b) = 7a – 3a + 5b = 4a + 5b
⇒ Si un paréntesis es precedido por un signo negativo (-), este se suprime cambiando los signos de los terminos que están dentro del paréntesis.
Ejemplo:
12a – (4a – 6b) = 12a – 4a + 6b = 8a + 6b
⇒ Si un paréntesis está precedido por una multiplicación, se utiliza la propiedad distributiva de la multiplicación respecto de la adición, es decir el término que está multiplicando, lo hace por cada término que está dentro del paréntesis.
Ejemplo:
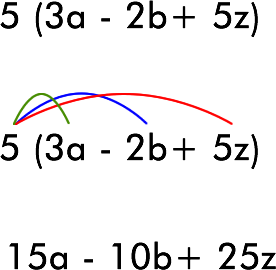
1.3- Ejercicios:
Elimine paréntesis y reduzca términos semejantes:
a) (2a + 3b) + (4a – 7b)
b) (a + 2b) – (7a – 3b)
c) [ 12 – (3x +4) ] – [7 + (8 -9x)]
d) (3a -2b + 5c) – (-3b -5c -3a)
e) 3x +2y – [x – (x-y)]
f) 3y – 2z- 3x- {x- [y- (z-x)] – 2x}

