1- Proporcionalidad Compuesta
Puede pasar que las variables en juego para una proporción sean más de dos, lo que provoca que la forma de analizar el problema sea un poco más complicada.
Ejemplo :
– Si 10 vacas comen 30 kilos de pasto en 20 días, ¿Cuántos kilos de pasto comerán 15 vacas en 10 días?.
Respuesta :
Como puedes ver las variables en juego son ahora tres, el número de vacas, la cantidad de kilos de pasto y el número de días. Para comenzar es bueno esquematizar el problema como sigue:
Vacas Kilos Días
10 → 30 → 20
15 → x → 10
Para resolver este tipo de ejercicios te recomendamos utilizar el siguiente método.
Iguala una de las columnas procurando hacer la corrección sobre las variables de la fila que corregiste, esto quiere decir si por ejemplo queremos igualar el número de días, o aumentamos al doble las vacas, o aumentamos al doble los kilos de pasto, ya que si 15 vacas comen x kilos en 10 días, entonces 15 vacas comerán 2 x kilos en 20 días (el doble de comida en el doble de tiempo), luego la proporción la podemos cambiar por:
Vacas Kilos Días
10 → 30 → 20
15 → 2x → 20
Luego, cuando tenemos una columna igualada ese valor pasa a ser un dato más del problema, ya que no existe diferencia entre una situación y la otra. Entonces ahora la pregunta es: ¿Si 10 vacas comen 30 kilos de pasto, ¿Cuántos kilos de pasto comerán 15 vacas?.
Vacas Kilos
10 → 30
15 → 2x
Simplemente eliminamos la columna que coincidía. Y nos queda una proporción de dos magnitudes, que es directamente proporcional (mientras más vacas, más pasto comen), y que ya sabemos resolver.
10 • 2x = 30 • 15
20x = 450
x = 450/20
x = 22,5 kilos
Otra forma de resolver este mismo problema es la siguiente:
– Si 10 vacas comen 30 kilos de pasto en 20 días, ¿Cuántos kilos de pasto comerán 15 vacas en 10 días?.
Paso 1: Hacer una tabla con los datos que te dan:
|
Vacas |
Kilos de pasto |
Días |
|
10 |
30 |
20 |
|
15 |
x |
10 |
Paso 2: Comparar cada columna con la de la incógnita. Con esto sabremos si la relación de proporcionalidad es inversa o directa.
Primero vamos a comparar la columna de la cantidad de vacas con la columna de la incógnita (kilos de pasto) En este caso nos damos cuenta que la relación de proporcionalidad es directa, ya que a más vacas, más kilos de pasto.
Vamos a utilizar la técnica de los signos para poder obtener la respuesta, esta dice:
Proporción directa, los signos son :
Proporción inversa, los signos son :
Valor que acompaña la incógnita siempre será positivo:
Esto se aplica de la siguiente manera:
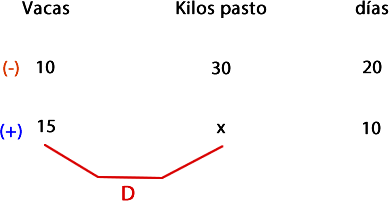
Paso 3: Ahora realizamos el mismo procedimento con la segunda columna (días) y la relacionamos con la de la incógnita (kilos de pasto). Nos damos cuenta que la relación es directa ya que al disminuir la cantidad de días, disminuyen los kilos de pasto que se necesitan.
Cuando la proporción es directa se anota al lado de la columna, los signos – y + como aparece en la imagen:
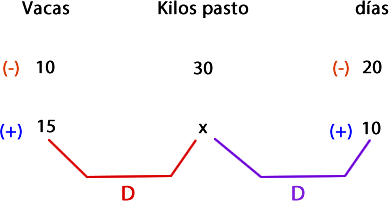
Luego en la columna de la incógnita, siempre se pone un signo (+) al lado del número.

Paso 4: Ahora determinamos el valor de x. Debes poner todos los valores que marcaste como positivos en el numerador y los negativos en el denominador, de la siguiente manera.
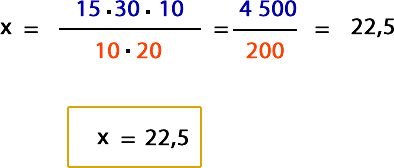
Luego la resuesta es: Comerán 22,5 kilos de pasto en 10 días.

