1- ¿Qué son los productos notables?
Los productos notables son fórmulas que permiten efectuar multiplicaciones indicadas, sin aplicar los criterios generales de la multiplicación algebraica, es decir, sin tener que multiplicar término a término.
Los productos notables cumplen reglas fijas donde el resultado puede ser escrito sin verificar la multiplicación.
Los productos notables que vamos a estudiar son 4, cuadrado de un binomio, cubo de un binomio, suma por su diferencia y binomios con un término en común.
1-1 Cuadrado de un binomio:
La fórmula que se utiliza cuando tienes un cuadrado de un binomio es la siguiente:
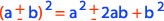
Si comprobamos esta fórmula tenemos que:

Entonces, el cuadrado de la suma o diferencia de dos cantidades, es igual al cuadrado de la primera cantidad, más o menos (según corresponda) el duplo de la primera cantidad por la segunda, más el cuadrado de la segunda cantidad.
Ejemplos:
a) x+52=x2+2x·5 +52 =x2+10x+25
b) 2x-122=2×2-22x·12+122=4×2-42x+14=4×2-2x+14
1.2- Cubo de un binomio
Cuando sumas o restas un binomio y lo elevas al cubo, puedes ocupar la siguiente fórmula:
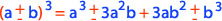
Si comprobamos esta fórmula tenemos que:

Entonces, esta fórmula nos dice que, el cubo de la suma o diferencia de dos cantidades es igual al cubo de la primera, más o menos (según corresponda) el triple del cuadrado de la primera por la segunda, más el triple de la primera por el cuadrado de la segunda, más o menos (según corresponda) el cubo de la segunda cantidad.
Ejemplos:
a) 4x+53=4×3+3·4×2·5+3·4x·52+53=64×3+240×2+300x+125
b) x2-3y3=x23-3·x22·3y+3×2·3y2-3y3=x6-9x4y+27x2y2-27y3
1.3- Suma por su diferencia
Para obtener el producto de la suma por la diferencia de dos cantidades puedes ocupar la siguiente fórmula:
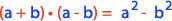
Si comprobamos esta fórmula tenemos que:
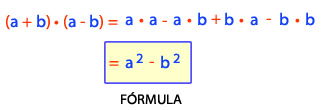
Entonces, la suma de dos cantidades multiplicada por la diferencia de estas, es igual a la diferencia de sus cuadrados.
Ejemplos:

1.4- Binomios con un término en común
Para el producto de dos binomios con un término en común se utiliza la siguiente fórmula:
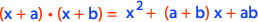
Si comprobamos esta fórmula tenemos que:
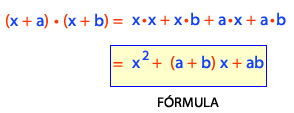
Entonces, el producto de dos binomios con un término en común es el primer término (común para los dos binomios) al cuadrado más la suma de los segundos términos de los binomios por el primer término en común más el producto de los segundos términos.
Ejemplos:
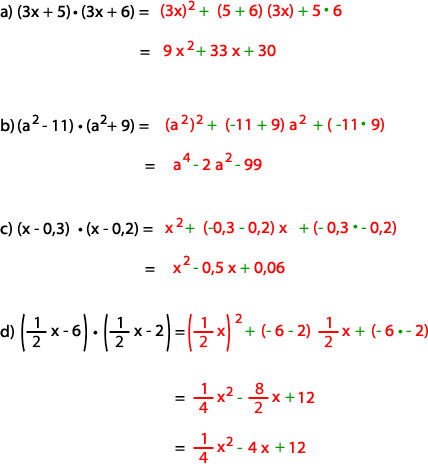
En estos ejemplos puedes ver que, independiente de los signos de los binomios, puedes ocupar la misma fórmula de binomios con un término en común.

