Por ejemplo, si disponemos de ampolletas de bajo consumo con potencias diferentes (8, 15 y 23 watt) y colocamos una por una en una lámpara, nos daremos cuenta de que, si bien todas las ampolletas permiten la transformación de energía eléctrica a energía lumínica y calor, algunas son capaces de otorgar una mayor energía en el mismo lapso. Por lo que la potencia corresponde a la cantidad de energía que los artefactos eléctricos pueden suministrar por unidad de tiempo.
La potencia eléctrica se mide en watt (W), en honor al inventor escocés James Watt (1736-1819) y su fórmula se expresa como:
i = es la intensidad de corriente eléctrica, medida en Ampere (A).
Como mencionamos, la unidad de medida de la potencia eléctrica es joule/segundo, lo que es equivalente a Watt, ya que:
| Fórmula para calcular la intensidad |
Recuerda que se mide en Ampere (A). |
| Fórmula para calcular la diferencia de potencial |
Recuerda que se mide en Volt (V). |
Veamos los siguientes ejemplos de ejercicios resueltos.
EJERCICIO 1
¿Cuál será la potencia o consumo en watt de una ampolleta conectada a una red de energía doméstica monofásica de 220 V, si la corriente que circula por el circuito de la ampolleta es de 0,45 Ampere?
Como nos están solicitando calcular la potencia, debemos utilizar la fórmula
Luego, debemos reconocer los datos que nos entregan.
V= 220 V.
i= 0,45 A.
Ahora, reemplazamos los datos en la fórmula.
P = 220 V • 0,45 A
P= 99 W 100 W.
Respuesta: La potencia de la ampolleta es de 99 W.
EJERCICIO 2
En casa, los enchufes poseen 220 V. Si sabemos que la potencia de una bombilla es de 100 W, ¿Cuál será la intensidad a través de la bombilla?
Como nos están solicitando calcular la intensidad, debemos utilizar la fórmula
Luego, debemos reconocer los datos que nos entregan.
V= 220 V.
P= 100 W.
Ahora, reemplazamos los datos en la fórmula.
i
Donde:
R = es la resistencia eléctrica del conductor, medida en Voltios/Ampere, lo cual es equivalente a la unidad llamada ohm (Ω).
V =es la diferencia de potencial eléctrico, medido en volt (V).
I =es la intensidad de la corriente, medida en ampere (A).
En función de la ley de Ohm planteada anteriormente, se establecen las siguientes relaciones despejando las variables:
| Fórmula para calcular la intensidad |
Recuerda que se mide en Ampere (A). |
| Fórmula para calcular la diferencia de potencial |
Recuerda que se mide en Volt (V). |
Veamos los siguientes ejemplos de ejercicios resueltos.
EJERCICIO 1
Si por una resistencia de 15 Ω circula una intensidad de 30 A, ¿Qué diferencia de potencial se creará?
Para resolver este problema, debes utilizar la fórmula , ya que nos están solicitando saber cuál es la diferencia de potencial.
Luego, debemos reconocer los datos que nos entregan en el planteamiento del problema.
R= 15 Ω
I= 30 A
Ahora, reemplazamos los datos en la fórmula.
V = 15 Ω • 30 A
V= 450 V
Respuesta: Se creará una diferencia de potencial de 450 V.
EJERCICIO 2
Calcula la intensidad de la corriente en este circuito.
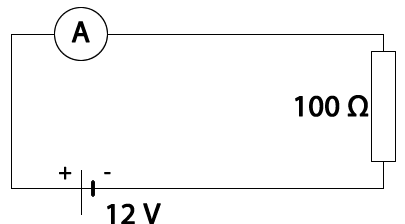
En este caso, debemos utilizar la fórmula
Reconocemos los datos.
V= 12 V.
R= 100 Ω.
Reemplazamos los datos en la fórmula.
Respuesta: La intensidad de este circuito es de 0,12 A.
3- Energía Eléctrica
Para determinar la energía eléctrica transformada o “disipada” de un determinado artefacto, debemos conocer su potencia eléctrica y el tiempo, aplicando la siguiente relación:
E = P • t
Donde:
E es la energía eléctrica.
P es la potencia.
t es el tiempo.
La energía eléctrica puede medirse en joule (j), pero habitualmente se mide en kilowatt-hora (kWh).
Observemos las siguientes equivalencias:
|
Energía |
Potencia |
Tiempo |
|
1 kWh = |
1 kW • |
1 h |
|
1 kWh = |
1000 W • |
3600 s |
|
1 kWh= 3,6 x 106 J |
||
Veamos los siguientes ejercicios resueltos.
EJERCICIO 1
En el hogar, un refrigerador se conecta a 220 V. Su potencia es de 200 W. ¿Cuál es la energía consumida por el refrigerador en 5 horas?
Para calcular la energía consumida, debemos utilizar la fórmula E = P • t
Luego, identificamos los datos.
P = 200 W.
t = 5 horas.
Reemplazamos los datos anteriores en la fórmula.
E = 200 W • 5 h.
E = 1000 W-h.
Por lo tanto, se consumen 1000 W en 5 horas. Si necesitamos transformar el resultado de Wh a kWh, debemos dividir el resultado por 1000, ya que: 1 kWh = 1000 Wh
Entonces, si dividimos 1000 wh por 1000, nos da como resultado 1 kWh.
Resultado: En 5 horas, el refrigerador consumió 1000 W-h, lo que es equivalente a 1 kWh.
EJERCICIO 2
En el hogar, un televisor se conecta a 220 V. Su potencia es de 120 W. ¿Cuál es la energía consumida por el televisor en 2 horas?
Para calcular la energía consumida, debemos utilizar la fórmula E = P • t
Luego, identificamos los datos.
P = 120 W.
t = 2 horas.
Reemplazamos los datos anteriores en la fórmula.
E = 120 W • 2 h.
E = 240 W-h.
Por lo tanto, se consumen 240 W en 2 horas. Si necesitamos transformar el resultado de Wh a kWh, debemos dividir el resultado por 1000, ya que debes recordar que 1 kWh es equivalente a 1000 Wh.
Resultado: El televisor en dos horas, consume 240 W-h, lo que es equivalente a 0,24 kWh.
Cuando circula una corriente eléctrica a través de un material, parte de la energía que transportan las cargas se transforman, inevitablemente, en calor. Experimentalmente se ha podido comprobar que la cantidad de energía eléctrica que se transforma en calor por este efecto, depende de la intensidad de corriente que circule y de la resistencia eléctrica del material.
Q = i2 • R • t
Donde:
R= resistencia en ohm (Ω)
i = intensidad de corriente en ampere (A)
t = tiempo en segundos (s).
Por lo tanto, la fórmula que nos entregará el valor en calorías es la siguiente:
Q = 0,24 • i2 • R • t
Revisemos el siguiente ejercicio resuelto.
Por la resistencia de 30 Ω de un artefacto eléctrico, circula una corriente de 4 A. Además, este aparato se encuentra conectado a una diferencia de potencial de 120 V. ¿Qué cantidad de calor (en calorías) se produce en 10 minutos?
Para resolver este ejercicio, debemos utilizar la fórmula Q = 0,24 • i2 • R • t que nos entrega el valor en calorías.
Identificamos los datos:
I= 4 A.
R = 30 Ω.
t = 10 minutos, lo que es equivalente a 600 segundos.
Reemplazamos los datos identificados en la fórmula:
Q= 0,24 • (4 A)2 • (30 Ω) • (600 seg)
Q = 69120 calorías.
Respuesta: Se generan 69120 calorías.
5- ¿Qué características poseen los artefactos eléctricos?
En cada artefacto eléctrico, se señala el voltaje, la frecuencia, la potencia, entre otros detalles. En Chile, el voltaje que utilizan los electrodomésticos corresponde a 220 V y la frecuencia es de 50 Hz.
En la siguiente tabla, se señalan como ejemplo ciertos artefactos eléctricos que podemos encontrar en nuestros hogares. Recuerda que el consumo energético de cada artefacto puede calcularse con la fórmula de la energía eléctrica o disipada que estudiamos anteriormente E = P • t.
Observa la siguiente tabla.
|
Artefacto eléctrico |
Potencia (W) |
Consumo energético en una hora (kWh) |
|
Aspiradora |
1.000 |
1 |
|
Computador |
400 |
0,4 |
|
Lavadora |
500 |
0,5 |
|
Estufa eléctrica |
2.000 |
2 |
|
Secador de pelo |
1.500 |
1,5 |
E = P • t
E = 1.500 W • 1 h
E = 1.500 Wh.
Si convertimos 1.500 Wh a kWh, nos quedaría que el secador de pelo gasta 1,5 kWh. Entonces, si queremos convertir de Wh a kWh, debemos dividir el valor por 1000.
A modo de conclusión, el electrodoméstico que consume más energía corresponde a la estufa eléctrica, ya que gasta 2 kWh. Por otra parte, el electrodoméstico que consume menos energía corresponde al computador, ya que gasta 0,4 kWh.

