Números reales y sus propiedades

1- ¿Qué son los números reales?

Los números reales son la unión del conjunto de los números racionales

ℚ

con el conjunto de los números irracionales

𝕀

recibe el nombre de conjunto de los números reales, y se denota con el símbolo:

ℝ

El conjunto de los números reales está formado por una serie de subconjuntos de números que definiremos a continuación:

– Los números naturales que surgen con la necesidad de contar

ℕ=1,2,3,4…

–  Los números enteros que complementan a los naturales pues contienen a los negativos y el cero.

ℤ=…-3,-2,-1,0,1,2,3…

–  El conjunto de los Números Racionales

ℚ

que corresponden a la unión de todos los números cuya expresión decimal es finita, infinita periódica o infinita semiperiódica. Es decir, el conjunto de los números racionales está compuesto por todos los números que pueden ser escritos como una fracción cuyo numerador y denominador (distinto de cero) son números enteros.

Ejemplo: 

ℚ=…-34,-12,-14,0,14,12,34…

– El conjunto  de los Números Irracionales

𝕀

que está formado por la unión de todos los números que admiten una expresión infinita no periódica.

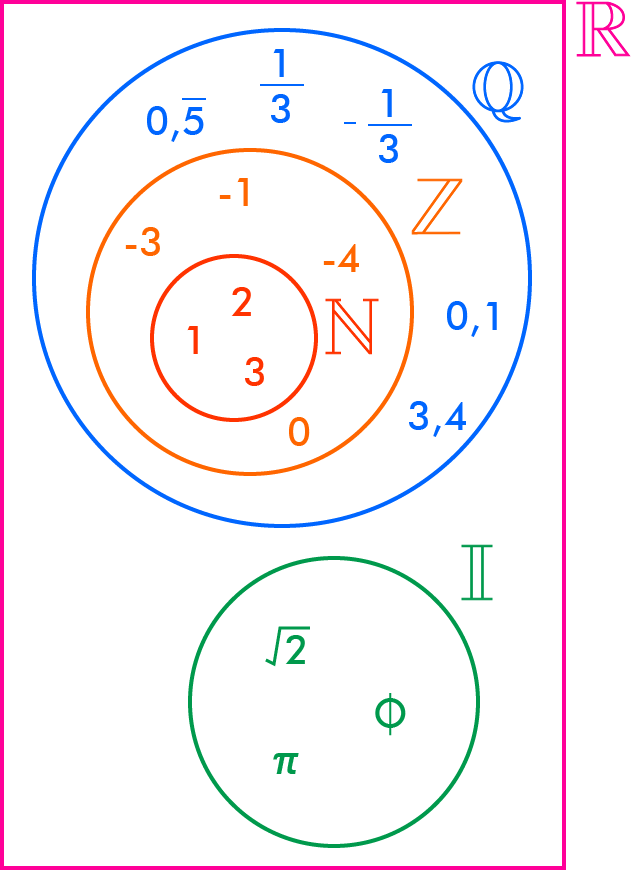
Puesto que los naturales están incluidos en los enteros y todos los enteros pueden ser representados como un número racional, se dice que los números reales son la unión de los números racionales y los irracionales.

2- Propiedades

2.1- Propiedades de la suma:

a) Propiedad Interna:
El resultado de sumar dos números reales es otro número real.

b) Propiedad Asociativa:
Si se tienen más de dos sumandos, da igual cuál de las sumas se efectúe primero. Si a, b y c son tres números reales:

Ejemplos: 

0,021 + (0,014 + 0,033) =  (0,021 + 0,014) + 0,033

c) Propiedad Conmutativa:
El orden de los sumandos no altera la suma.

Ejemplos:

3 ∈ R, 4 ∈ R

→

3 + 4 = 4 + 3

3

∈ R, 9 ∈ R

→

3

+ 9 = 9 +

3

Ejemplos:

2.2- Propiedades de los reales en la resta o sustracción

Al efectuar sustracciones o restas deben considerarse las siguientes reglas de los signos:

a) Si el minuendo y el sustraendo son positivos, y el minuendo es mayor que el sustraendo, se efectúa la resta y el resultado es positivo.

Ejemplo:

28,7 – 11,2 = 17,5

b) Si el minuendo y el sustraendo son positivos, y el minuendo es menor que el sustraendo, se efectúa la resta y el resultado es negativo.

Ejemplo:

11,2 – 28,7 = –17,5

c) Si el minuendo es negativo y el sustraendo es positivo, se efectúa la suma de ambos números y al resultado se le pone el signo menos.

Ejemplo:

– 28,1 – 11,2 = – 39,3

d) Restar un número positivo es lo mismo que sumar un número negativo.

Ejemplo:

28,7 – 11,2 = 28,7 + (– 11,2) = 17,5

e)  Restar un número negativo es lo mismo que sumar un número positivo.

Ejemplo:

28,7 – ( – 11,2) = 28,7 + 11,2 = 39,9

f) La resta no tiene todas las propiedades de la suma:

La resta no es una operación conmutativa:

Ejemplo:

52,4 – 31,2 = 21,2, y ese resultado es distinto de 31,2 – 52,4 = – 21,2

2.3- Propiedades de la multiplicación

La multiplicación tiene las siguientes propiedades:

a) Propiedad interna:
El producto de los números reales, es un número real.

–  Es un conjunto denso, esto es, entre dos números reales siempre hay otro número real.

Los números racionales, cuando se escriben como números decimales, son finitos, infinitos periódicos o infinitos semiperiódicos. Sin embargo, los números irracionales son siempre números decimales infinitos pero no periódicos. Considerando su representación en la recta numérica, los números reales ocupan la recta numérica por completo, ya que los números irracionales completan todos los espacios dejados por los racionales en la recta numérica.

3- Igualdad en números reales

Dos números reales son iguales si tienen igual parte entera e igual parte decimal.

La igualdad en el conjunto

ℝ

cumple las siguientes propiedades:

Refleja:

Simétrica:

Transitiva :

4- Comparación de números reales

Dados dos números reales a y b, se dice que

a≥b

(a es mayor o igual que b) si

a -b

es un número real positivo o es cero.

Es decir:

a≥b ↔a-b≥0

– Teniendo en cuenta que todo número real se puede expresar como un número decimal, puedes establecer un orden para dos o más númerosreales comparando cifra a cifra.

Ejemplo:

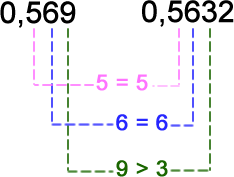
Comparemos 0,569 y 0,5632

Si comparamos cifra a cifra: