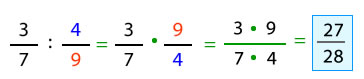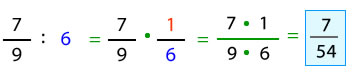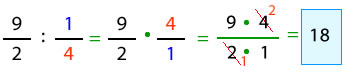1- Multiplicación de fracciones
1.1- Representación gráfica de la multiplicación de un número natural por una fracción
Al igual que en los números naturales, la multiplicación de fracciones se relaciona con expresar de manera abreviada una suma iterada.
se puede leer como dos veces tres séptimos.
se representa 2 veces.
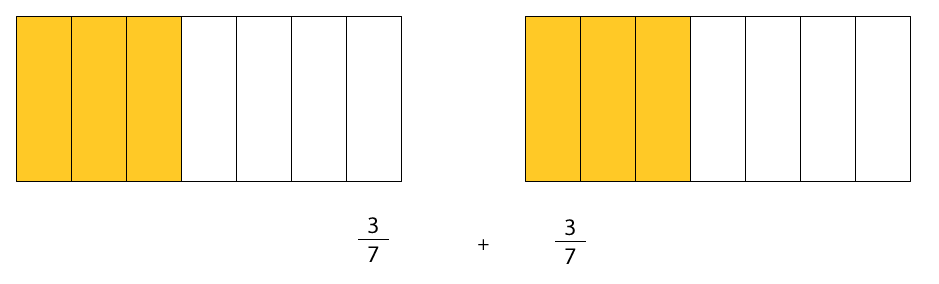
Luego, se junta todo en una misma representación resultando .
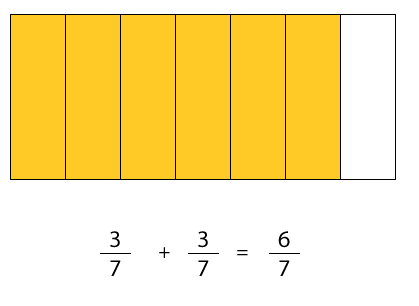
Finalmente, la expresión puede desarrollarse de la siguiente manera:
Se escribe un 1 debajo del número 2, luego se multiplican los numeradores 2 y 3. Por último se multiplican los denominadores 1 y 7.
La expresión no se puede simplificar.
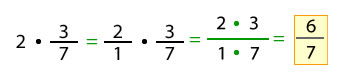
Resolver el siguiente problema:
En una tienda hay 80 botellas de agua de 1/4 L cada una. ¿Cuántos litros de agua hay en total?
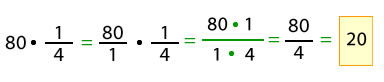
Respuesta: En total hay 20 L de agua en la tienda.
1.2- Representación gráfica de la multiplicación de una fracción por otra fracción
Lee la siguiente situación:
En un terreno se disponen de la superficie para cultivar, de esta superficie se destinará para el cultivo de papas. ¿Cuánta superficie del total será ocupada para el cultivo de papas?
Primero se representa la superficie destinada para cultivar que corresponde a .
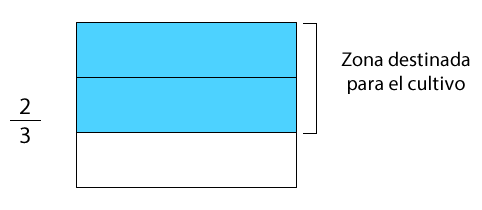
Luego, se divide el modelo en 5 barras verticales para representar .
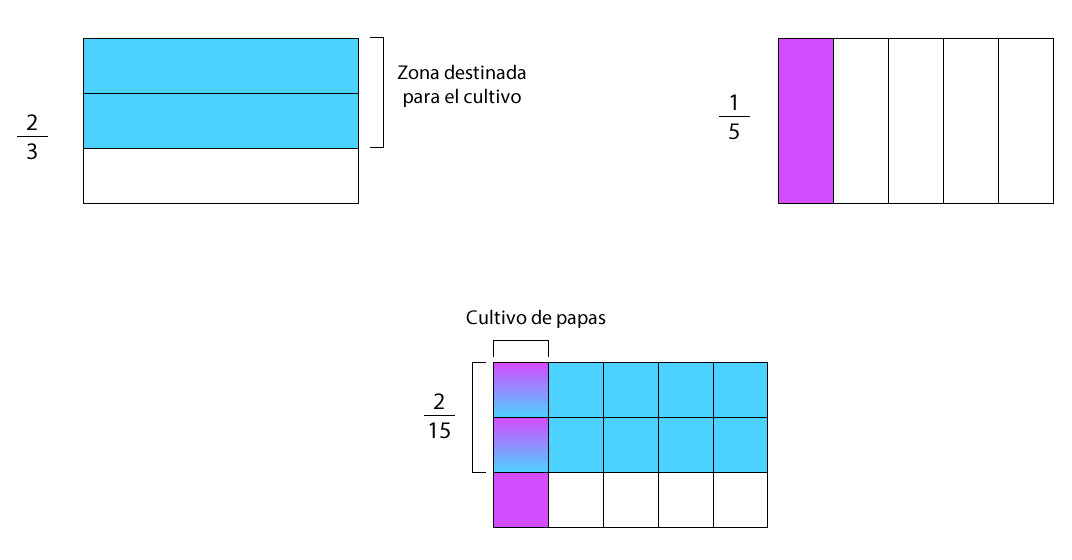
Finalmente, el área de intersección donde se mezclan los dos colores, corresponde al producto de las fracciones.
En este caso, se destinan para cultivar papas.
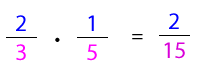
Para multiplicar fracciones, se multiplican los numeradores entre sí y se multiplican los denominadores entre sí. Luego, si es necesario, se simplifica la fracción resultante.
Observa otro ejemplo:
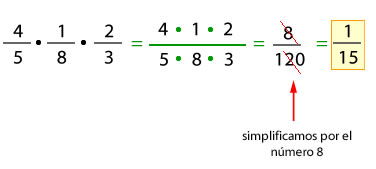
1.3- Resolución de problemas
Ejemplo:
Don José dejó 3/5 de la pared para pintar con colores cálidos. Si pintará de color café 2/3 de lo destinado a los colores cálidos, ¿qué parte de la pared será de color café?
Si representamos gráficamente la información tenemos:
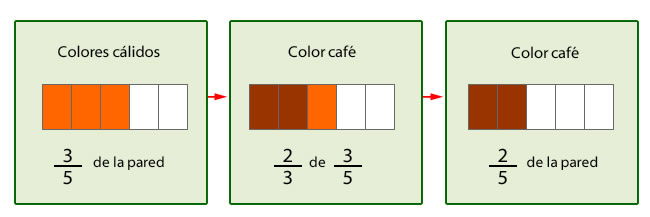
Por lo tanto, se tiene que 2/5 de la pared serán pintados de color café.
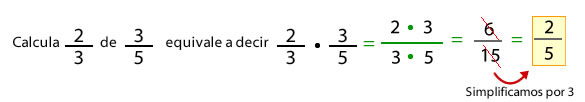
2- División de fracciones
2.1- Representación gráfica de la división de un número natural por una fracción
En los números naturales la división se relaciona con la idea de reparto equitativo o como medida. En el caso de las fracciones también se emplea esta idea.
Observa el siguiente ejemplo:
Camila tiene un envase de 3 litros de agua y los distribuye en vasos de litro cada una. ¿Cuántos vasos puede llenar?
La situación se puede representar de la siguiente manera:
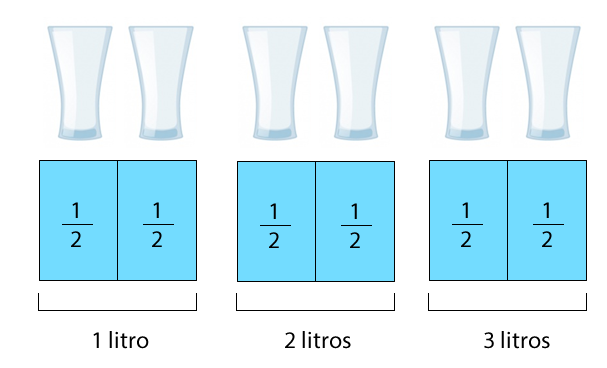
Se puede apreciar que con 3 litros de agua se pueden llenar 6 vasos de litro.
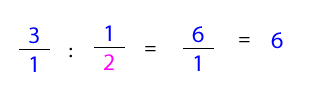
Para realizar la operación se escribe un 1 debajo del número 3, luego se multiplica de manera cruzada.
2.2- Representación gráfica de la división de una fracción por otra fracción
Lee la siguiente situación:
Un trozo de madera de m de largo se quiere cortar en trozos de m de largo. ¿Cuántos trozos de madera se obtendrán?
La situación se puede representar de la siguiente manera:
Primero se representa y debajo de este se representa . Ambos deben tener las mismas dimensiones.
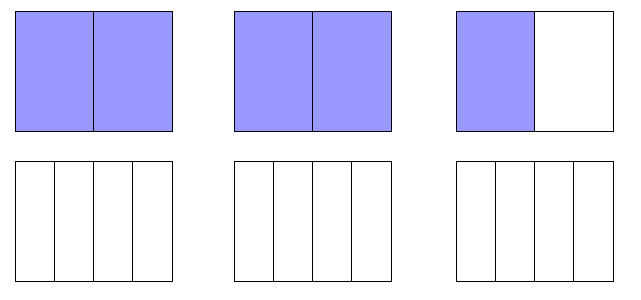
Luego, se observa cuántas veces "cabe" en .
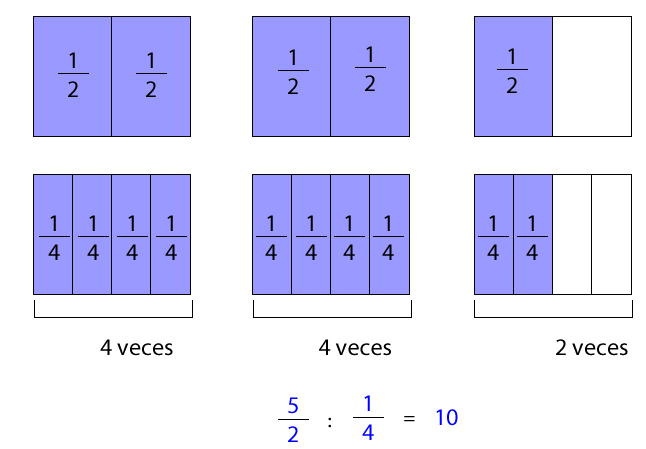
De acuerdo a la representación, "cabe" 10 veces en .
2.3- Procedimiento para dividir una fracción por otra fracción
Para dividir 2 fracciones, se multiplican sus términos en cruz, es decir, se multiplica el numerador de la primera fracción con el denominador de la segunda. Luego se multiplica el denominador de la primera fracción por el denominador de la segunda.