1- Introducción
En este tema estudiaremos sobre la función potencia, ¿qué significa?, cómo es su gráfica y sus propiedades.
La función potencia es aquella función que está compuesta de la siguiente manera:
y
En ella existe una constante «a» que amplifica la incógnita “” que es elevada a la potencia “”. (“” y “” corresponden a todos aquellos números reales )
Esta función al ser graficada puede tomar distintas formas dependiendo de los valores que se asignen a la constante “” y a la potencia “”.
1.1- Ejemplos de gráficas de función potencia
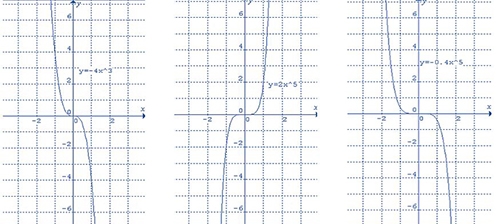
2- ¿Qué formas puede tomar la función potencia?
Sabemos que un gráfico está compuesto por dos ejes perpendiculares entre sí (X e Y) formándose 4 cuadrantes. La siguiente figura muestra la ubicación de cada uno de estos.
También se suelen nombrar con números Romanos.
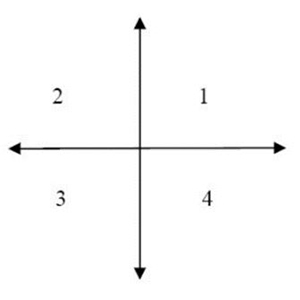
A continuación, veremos cómo se describen algunos escenarios más comunes gráficamente:
Escenario 1:
Cuando “” toma valores naturales y “” toma valor 1.
En este caso la función toma la forma de una línea recta con una inclinación de 45 grados respecto al eje X.
Si “” es un número natural, ocupará los cuadrantes 1 y 2.
Escenario 2:
Cuando “” toma valores naturales y “” toma valor 0.
En este caso la función toma la forma de una línea recta horizontal, paralela al eje X.
Si “” es un número positivo, ocupará los cuadrantes 1 y 3 y si “” es un número negativo, ocupará los cuadrantes 2 y 4.
Escenario 3:
Cuando “” toma valores naturales y “” toma valores naturales pares.
En este caso la función es simétrica respecto al eje Y. Ocupando los cuadrantes 1 y 2.
Escenario 4:
Cuando “” toma valores naturales y “” toma valores naturales impares, distintos de 1. En este caso la función es simétrica respecto al origen. Ocupando los cuadrantes 1 y 3.
3- ¿Cómo estudiaremos la gráfica de la función potencia?
Generalmente, cuando se estudia la representación gráfica de una función, se realiza mediante una tabla de valores y luego se ubican puntos coordenados en un plano cartesiano.
En este caso, resulta complejo, ya que se tendrían que evaluar demasiados valores para x. Por lo tanto, ubicar demasiados puntos coordenados.
Para realizar el estudio más fácil, determinaremos la representación gráfica solo analizando elementos e información de la función .
3.1- Casos dentro de la función potencia
Existen diferentes casos dentro de una función potencia, dependiendo de si n es un (número entero positivo) o si n es un (número entero negativo).
Dentro de ambas situaciones se analiza primero si a es positivo o negativo y segundo si n es par o impar.
Todos estos datos los entrega la función de gráfica original.
3.2- Desplazamiento de la función
Si la función es de la forma , su gráfica corresponderá a la de , donde analizaremos si el desplazamiento es horizontal o vertical.
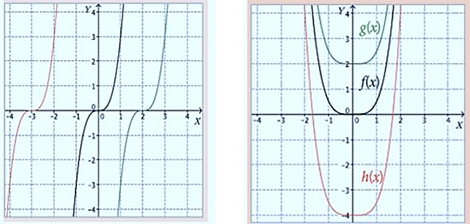
Ejemplo horizontal Ejemplo Vertical
4-¿Cómo determinar una gráfica a partir de la función?
Caso 1:
con
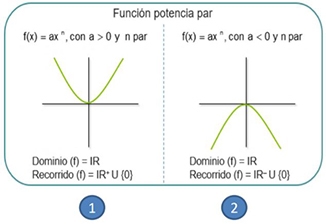
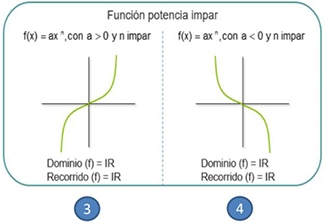
Si en una función , n es positivo se infieren como función original los 4 tipos de gráficas.
Si en una función , n es par entonces las opciones se reduce a 2 tipos de gráficas (1 y 2) y se analiza es positivo se reduce a la gráfica 1, si es negativo se reduce a la gráfica 2 como función original.
Si en una función , n es impar entonces las opciones se reduce a 2 tipos de gráficas (3 y 4) y se analiza es positivo se reduce a la gráfica 3, si es negativo se reduce a la gráfica 4 como función original.
Veamos algunos ejemplos:
Ejemplo 1:
Sea . Analizaremos que gráficas nos sirven como opción:
| Si n es positivo |
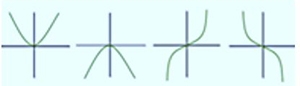 |
| Si n es par |
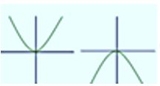 |
| Si es negativo |
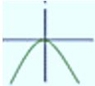 |
Luego la gráfica original o base, será:

Ejemplo 2:
Sea . Analizaremos que gráficas nos sirven como opción:
| Si n es positivo |
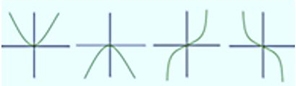 |
| Si n es impar |
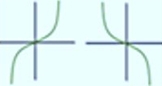 |
| Si es positivo |
 |
Luego la gráfica original o base, será:

Caso 2:
con
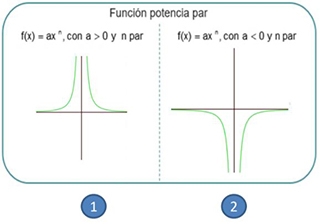
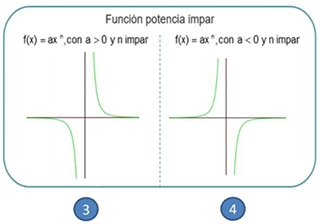
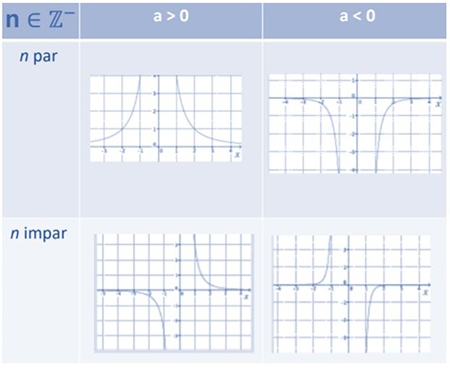
Si en una función , n es negativo se infieren como función original los 4 tipos de gráficas.
Si en una función , n es par entonces las opciones se reduce a 2 tipos de gráficas (1 y 2) y se analiza es positivo se reduce a la gráfica 1, si es negativo se reduce a la gráfica 2 como función original.
Si en una función , n es impar entonces las opciones se reduce a 2 tipos de gráficas (3 y 4) y se analiza es positivo se reduce a la gráfica 3, si es negativo se reduce a la gráfica 4 como función original.
Veamos algunos ejemplos:
Ejemplo 1:
Sea
Analizaremos que gráficas nos sirven como opción:
| Si n es negativo |
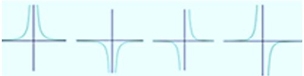 |
| Si n es impar |
 |
| Si es negativo |
 |
Luego la gráfica original o base, será:
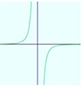
Ejemplo 2:
Sea .
Analizaremos que gráficas nos sirven como opción:
| Si n es negativo |
 |
| Si n es impar |
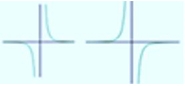 |
| Si es positivo |
 |
Luego la gráfica original o base, será:
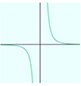
5- Resumen
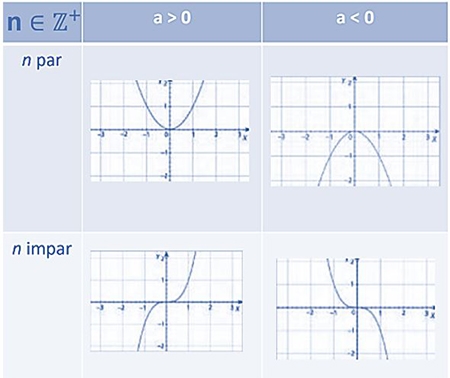
Ejemplo:
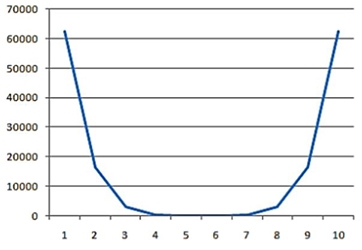
Considera la función . Vamos a completar la tabla de valores y dibujar el gráfico:
- Si
- Si
- Si
Así sucesivamente, calculamos el valor de y reemplazando el correspondiente valor de x y completamos la tabla de valores. Luego graficamos y obtenemos:
| x | y |
| -5 | 62.500 |
| -4 | 16.384 |
| -3 | 2.916 |
| -2 | 256 |
| -1 | 4 |
| 1 | 4 |
| 2 | 256 |
| 3 | 2.916 |
| 4 | 16.384 |
| 5 | 62.500 |
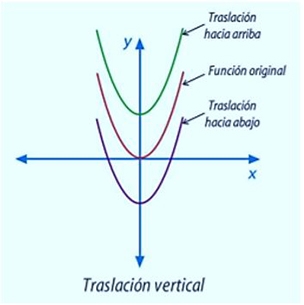
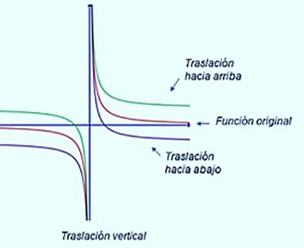
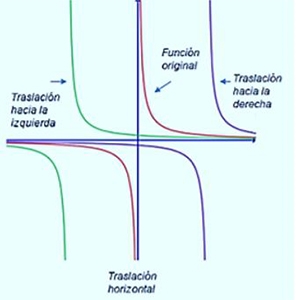
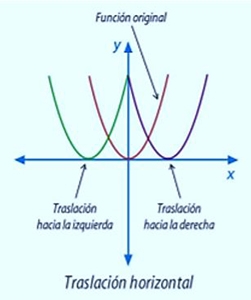
5.1- Traslación de la Función Potencia
Si la función es de la forma , entonces su gráfica corresponderá a la de , pero desplazada h unidades horizontalmente (a la izquierda si y a la derecha si ) y k unidades verticalmente (hacia abajo si y hacia arriba si ).
Ejemplos de traslaciones vertical y horizontalmente:
Ejemplo:
1- Sea , determinar su gráfica:
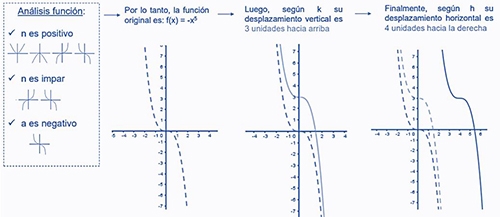
2- ¿Cuál es la función cuya gráfica es la siguiente?
A.
B.
C.
D.
E.
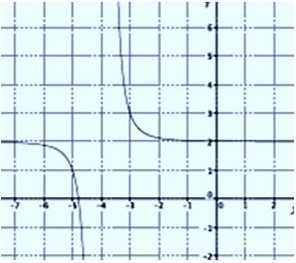
Según la gráfica, podemos deducir que:
- , luego n es negativo.
- n es impar, luego la función original es .
- es positivo, luego la función sería

