Función logarítmica

1- Función logarítmica

Recordemos que el logaritmo nos entrega el número por el cual hay que elevar la base para obtener un resultado específico. 

Por ejemplo, si queremos encontrar el valor de “Y” en la ecuación $b^y\text{=a, (con b > 0, b ≠1)}$ podemos calcularla mediante el logaritmo, expresándolo de la forma ${\log }_b\left(a\right)=y$, donde “a” es la potencia y “b” la base. 

Supongamos que ahora yo puedo elegir el valor que toma “a” en esa ecuación. Como es variable, la llamaremos “x”. Entonces, nos quedaría$y={\log }_b\left(x\right)$.

 
Ahora, “Y” es una función que depende del valor que tome x. es decir:

$F\left(x\right)= {\log }_b\left(x\right)$

Entonces, la función logarítmica es una función de la forma$F\left(x\right)= {\log }_b\left(x\right)$.

1.1-     Propiedades función logaritmo

$\to$Su dominio son todos los reales positivos $(x>0)$.

Esto es porque, por propiedad de los logaritmos, la base siempre es positiva $(b>0)$, entonces NO es posible que al elevar por “Y” a un número positivo nos dé como resultado un número negativo o cero. Por lo mismo, lo que está dentro del logaritmo siempre debe ser mayor que cero. 

$\to$Para $b>1$, Es una función creciente. Es decir, cuando aumenta el valor de la variable independiente x, también aumenta el valor de la variable dependiente Y. 

$\to$Para $0<b<1$, es una función decreciente. Es decir, cuando aumenta X, disminuye Y. 

 
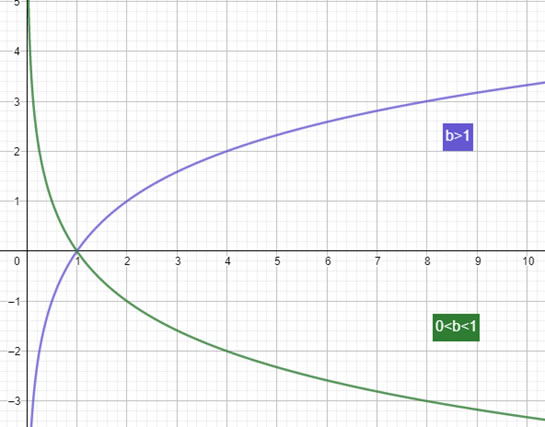
$\to$ La función cambia según el valor que tome la base “b”. A pesar de eso, todas ellas cortan al eje x en el punto (1,0).

Esto es por la propiedad de los logaritmos, ${\log }_b\left(1\right)=0$. 

2- Traslación de funciones

Una traslación es un movimiento de la función dentro del plano cartesiano, pero sin cambiar su forma.  

2.1-Traslación horizontal
A la función le sumamos un número “c” dentro del logaritmo. Lo que esto generará en la función es que se mueva horizontalmente en el plano cartesiano. Entonces, ahora la función logaritmo será:

$F\left(x\right)= {\log }_b(x+c)$

$\to$Si $c>0$, la función se trasladará hacia la izquierda
$\to$Si $c<0$, la función se trasladará hacia la derecha
$\to$El dominio de la función pasa a ser $x>–c$

¿Por qué?
Por ejemplo, tenemos la función $h\left[x\right]={\log }_5(x+3)$. Necesitamos un valor de X tal que $h\left[x\right]=0$. ¿Qué valor cumple esta condición?

Antes, sin sumarle nada dentro del logaritmo, teníamos que $f\left[x\right]= {\log }_5\left(x\right)$. Por propiedad, sabemos que la función toma el valor de 0 cuando ${\log }_5\left(1\right)$.  Sin embargo, con la nueva función $h\left[x\right]$ ya no se cumple esta propiedad, ya que $h\left[1\right]= {\log }_5(1+3)$, lo cual NO es 1. 

Lo que necesitamos, es que dentro del logaritmo obtengamos el valor de 1. Entonces, el valor que cumple esto es$x=–2$, ya que $h[–2]= {\log }_5(–2+3)= {\log }_5\left(1\right)=0$. Es decir, ahora se ha movido el valor de x tres unidades hacia la izquierda en el plano cartesiano con respecto a la función original.  

De la misma manera, si evaluamos la función $g\left[x\right]= {\log }_5(x–3)$, para obtener el valor $g\left[x\right]=1$ necesitamos un valor de x igual a 4. Es decir, se ha movido el valor de x tres unidades hacia la derecha en el plano cartesiano con respecto a la función original. (En el ejemplo, $b>1$)

2.2-Traslación vertical
A la función le sumamos un número “c” fuera del logaritmo. Lo que esto generará en la función es que se mueva verticalmente en el plano cartesiano. Entonces, ahora la función logaritmo será:

$F\left(x\right)= {\log }_b\left(x\right)+c$

$\to$ Si $c>0$, la función se trasladará hacia arriba.
$\to$ Si $c<0$, la función se trasladará hacia abajo.

 
¿Por qué?
Por ejemplo, tenemos la función $J\left[x\right]= {\log }_5\left(x\right) + 3$ y la función $f\left[x\right]= {\log }_5\left(x\right)$. ¿Qué valor toma las funciones anteriores con x=1?

Evaluamos cada función:

$F\left[1\right]= {\log }_5\left(1\right)=0$

$J\left[1\right]= {\log }_5\left(1\right) + 3 = F\left[1\right] + 3 = 3$. 

Es decir, es lo mismo que la función original, pero sumándole 3 unidades. La función es trasladada hacia arriba al agregarle 3 unidades al eje Y. 

De la misma manera, si evaluamos la función $K\left[x\right]= {\log }_5\left(x\right)–3$, el resultado será el mismo que la función original, pero restándole 3 unidades. Es decir, la función es trasladada hacia abajo al restarle 3 unidades al eje Y. 

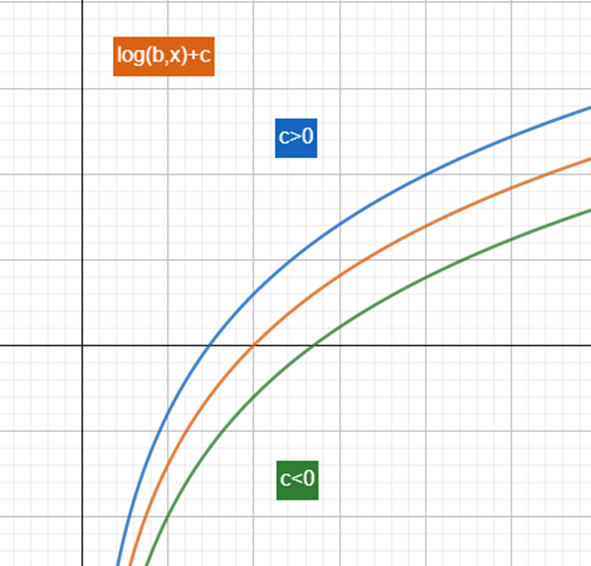
Gráficamente el cambio se ve de la siguiente manera (En el ejemplo, $b>1$):

 
Ejemplo

1- Grafique la función $F\left[x\right]={\log }_e(x–e)$.  

Para poder graficar una función logaritmo, debemos responder a las siguientes preguntas:

$\to$¿Es creciente o decreciente?

$\to$¿Tiene traslación horizontal o vertical?

$\to$¿Cuál es el corte con el eje X?

Solución:
La función ${\log }_e\left(x\right)$, con base “e” es conocida como logaritmo natural. “e” es un número que equivale aproximadamente 2,7182. 

– Como la base es mayor a 1, sabemos que la función es creciente. 

– Como la función es de la forma ${\log }_b(x+c)$, con $c<0$, hay una traslación horizontal hacia la derecha. 

– El corte con el eje X se dará cuando $F\left[x\right]=0$. Entonces, despejamos la función:

$0= {\log }_e(x–e)$

Por propiedad, ${\log }_b\left(1\right)=0$. Entonces, buscamos que $x–e=1$. Despejando, obtenemos que $x=1+e$. Por lo tanto, el corte con el eje X es en el punto $\left(\text{1+e, 0}\right)$. 

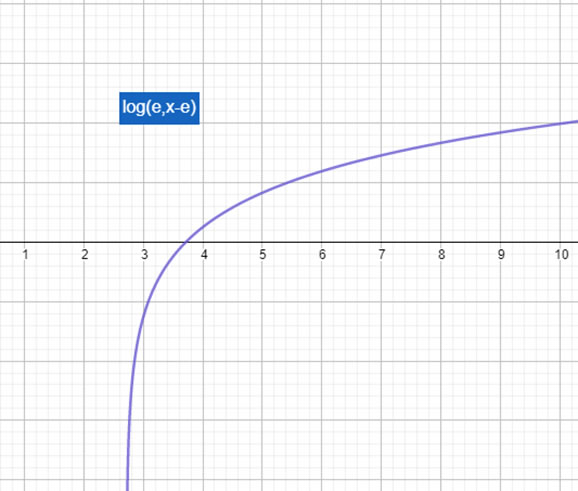
Entonces, el gráfico más o menos sería de la siguiente forma: 

Ejemplo
2- Sea la función $G\left[x\right]= {\log }_{0,5}(x+2) + 5$. Determine:

$\to$ ¿Es creciente o decreciente?

$\to$¿Qué tipo de traslación tiene?

$\to$¿Cuál es el corte con el eje X?

$\to$¿Cuál es el dominio de la función?

Solución:
Como la base del logaritmo está entre 0 y 1, el logaritmo es decreciente. También, vemos que tiene una traslación horizontal hacia la izquierda, y una traslación vertical hacia arriba. Por último, el corte con el eje lo encontramos al despejar x de $G\left[x\right]=0$.

$$\begin{gathered} {\log }_{0,5}(x+2) + 5 = 0 \\ {\log }_{0,5}(x+2) = –5 \end{gathered}$$

Para resolver esta ecuación, expresamos $–5$ como un logaritmo en base 0,5. Entonces, decimos que $–5 = \log 0,5(0,5–5) = \log 0,5\left(32\right)$

Entonces, 

${\log }_{0,5}(x+2) = {\log }_{0,5}\left(32\right)$

Como ambos lados están expresados solo con logaritmos de la misma base, Igualamos las potencias y nos queda que:

$$\begin{gathered} X+2=32 \\ X=30 \end{gathered}$$

Por lo tanto, el corte con el eje X se da en el punto $(30,0)$

Por último, con una traslación horizontal, el dominio de la función cambia. Ahora, será $x>e$.

3-Transformación de funciones

$\to$$F\left(x\right)= {\log }_b(–x)$

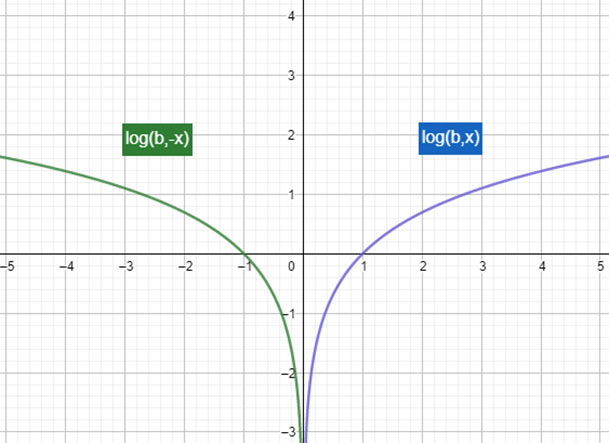
Ahora, la función tiene un signo negativo dentro del logaritmo. Recordemos que necesitamos que lo que esté dentro del logaritmo sea positivo. Para lograr eso, necesitamos que $x<0$. 

Gráficamente puede verse como un “reflejo” de la función original con respecto al eje Y. En el ejemplo, $b>1$. 

$\to$$F\left(x\right)= –{\log }_b\left(x\right)$

Ahora, la función tiene un signo negativo fuera del logaritmo. Lo que genera esta transformación, es que todos los valores de Y tengan el signo contrario al que tenía antes (ya que ahora al número se multiplica por -1). 

Gráficamente, se genera un “reflejo” con respecto al eje X. En el ejemplo, $b>1$. 

Ejemplo 
Dada la función: $L\left[x\right]= –{\log }_{0,5}(–x+3)$, responda:

$\to$¿Es creciente o decreciente?

$\to$¿Qué tipo de traslación o transformación tiene? 

$\to$Grafique.

Solución:
Para responder las preguntas, hay que analizar con cuidado cada parte de la función.

Podemos observar que la base del logaritmo es menor a 1, por lo que podríamos pensar que la función es decreciente. Sin embargo, como la función tiene una transformación al ser multiplicada por -1 fuera del logaritmo, hace que ahora sea una función creciente. 

Vemos que tiene una transformación dentro y fuera del logaritmo. Además, observamos una traslación. Como antes, podemos pensar que es una traslación hacia la izquierda. Sin embargo, como hay una transformación dentro del logaritmo, la traslación ahora es hacia la derecha. 

Es decir, si hay una transformación dentro del logaritmo, la propiedad de traslación horizontal cambia. Sin embargo, la propiedad de traslación vertical es igual para cualquier tipo de transformación. 

Gráficamente nos queda: