Elementos secundarios del triángulo: simetrales y transversales de gravedad

1- Elementos secundarios de un triángulo

Los elementos secundarios son las alturas, bisectrices, simetrales y transversales de gravedad, de los cuales detallaremos a continuación las simetrales y transversales de gravedad;

 

2- Simetrales de un triángulo

Las simetrales o también llamadas mediatrices de un triángulo son las rectas perpendiculares que pasan por el punto medio de cada lado. El triángulo tiene tres simetrales, una por cada una de sus lados y se nombran con la letra s y un sub índice según la letra del vértice opuesto al cual se traza la simetral (ej.: s_a).

Las tres simetrales se cortan en un punto llamado circuncentro, la cual se abrevia con la letra C, el cual se encuentra a igual distancia de cada uno de los vértices del triángulo, y es el centro de la circunferencia circunscrita al triángulo.

– En un triángulo acutángulo, el centro de la circunferencia circunscrita está dentro del triángulo.

Ejemplo simetrales en un triangulo acutángulo:

Llamaremos medidas de las simetrales a los segmentos;

CN = s_a

CO = s_b

CM = s_c

C = Circuncentro

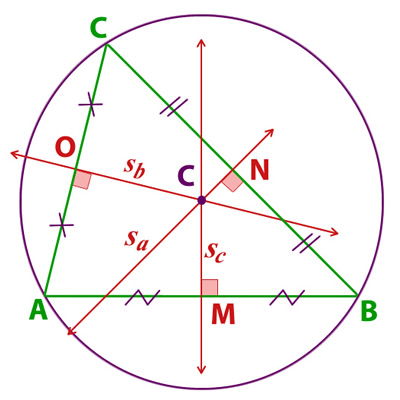
CA = CB = CC = radio de la circunferencia circunscrita al triangulo ABC.

Si te fijas el circuncentro se encuentra dentro del triángulo.

– En un triángulo obtusángulo, el centro de la circunferencia circunscrita está fuera del triángulo.

Ejemplo simetrales en un triangulo obtusángulo:

 

 

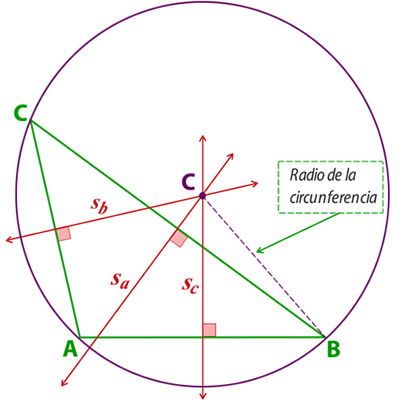
Si te fijas en este ejemplo, marcamos el radio de la circunferencia circunscrita al triángulo, para que notes que la distancia desde el centro C a los vértices es la misma.

– En un triángulo rectángulo, el centro de la circunferencia circunscrita es el punto medio de la hipotenusa (lado opuesto al ángulo recto).

Propiedad: Un triángulo es rectángulo si y solo si el centro de su circunferencia circunscrita es el punto medio de su hipotenusa.

Ejemplo simetrales en un triangulo rectángulo:

 

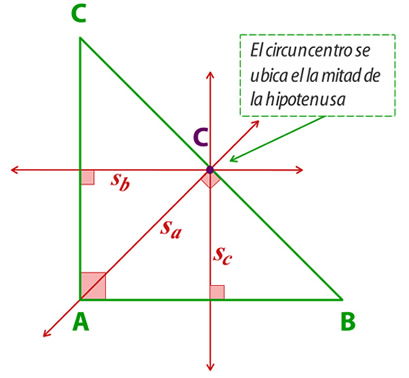
No es necesario que siempre dibujes la circunferencia circunscrita para saber que corresponde a la simetral del triángulo.

Fíjate en los ejemplos anteriores que, a diferencia de la altura, las simetrales no siempre pasan por el vértice opuesto.

Nota: Una circunferencia circunscrita al triángulo, quiere decir que es la circunferencia que pasa por todos los vértices de él, y contiene completamente al triángulo.

 

2.1- ¿Cómo dibujar las simetrales con regla y compás?

Para dibujar las simetrales de un triángulo ABC, tienes que realizar los siguientes pasos en cada uno de los lados, en este caso trazaremos la simetral del lado AB;

1° Utilizando el compás traza dos arcos, con la misma abertura, la cual tiene que ser mayor a la mitad del segmento AB;

– El primer arco trázalo con centro en A.

 

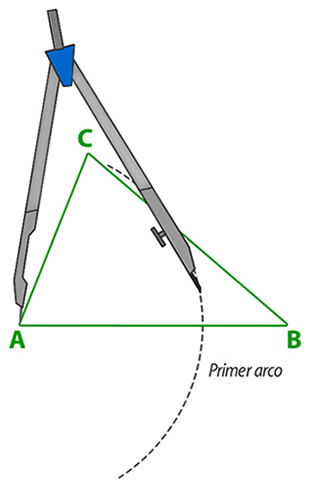
– El segundo arco con centro en B

 

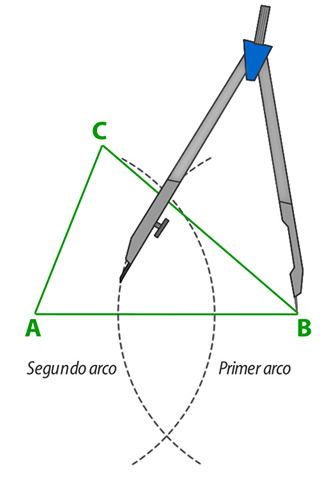
2° Traza una recta con una regla, que pase por los puntos de intersección de los arcos que dibujamos en el paso anterior.

 

 

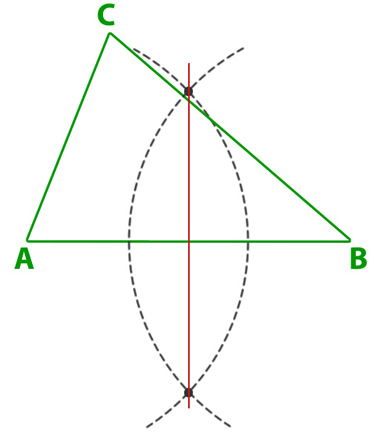
Esta recta corresponde a la simetral del lado AB, por lo tanto, lo divide en dos segmentos iguales y forma un ángulo de 90°.

 

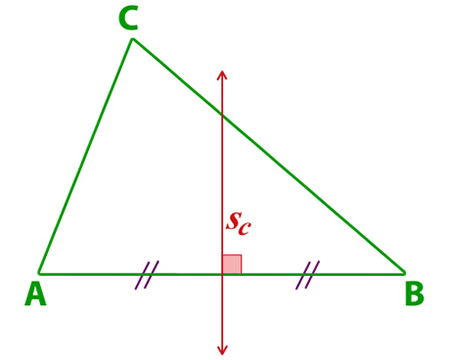
Para trazar las otras dos simetrales, debes seguir los mismos pasos en los lados BC y CA.

 

3- transversales de gravedad de un triángulo

Las transversales de gravedad de un triángulo son las rectas que unen cada vértice con el punto medio del lado opuesto. Un triángulo tiene tres transversales de gravedad, una por cada lado y se nombran con la letra t y un sub índice según la letra del vértice desde el cual se traza (ej.: t_a).

Las tres simetrales se cortan en un punto llamado baricentro o centro de gravedad, la cual se abrevia con la letra G.

Ejemplo transversal de gravedad:

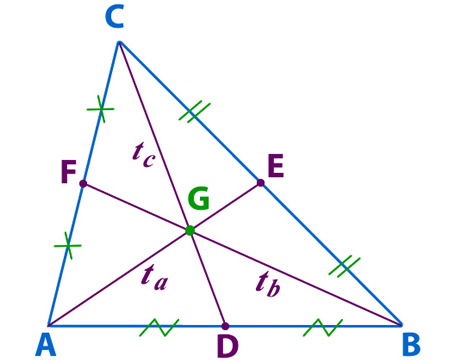
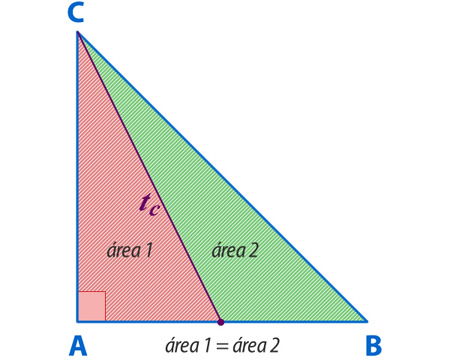
– Cada una de las transversales de gravedad divide al triángulo en dos triángulos de áreas iguales.

Ejemplo:

 

 

– La medida desde cualquiera de sus vértices hasta el baricentro, siempre será 2/3 de la distancia total de la transversal de gravedad.

 

Ejemplo:

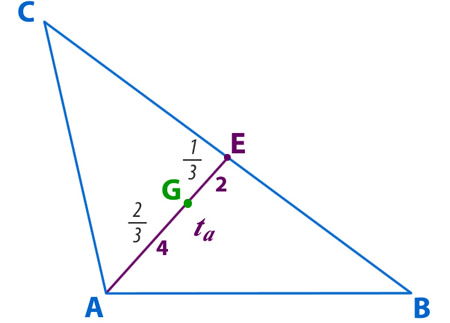
Si la transversal de gravedad t_a (recta AE) mide 6, la distancia desde el vértice A hasta el baricentro (G) será 2/3 de 6, es decir, 4 y la distancia desde G hasta E será 1/3 de 6, es decir 2.

 

 

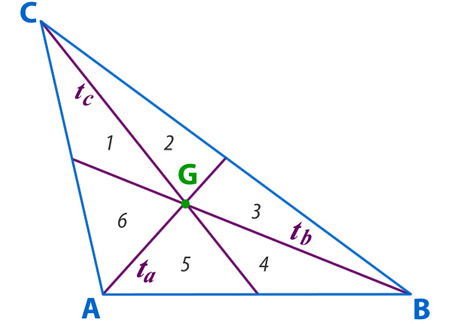
– Las tres transversales de gravedad dividen al triangulo en 6 triángulos de áreas iguales.

 

3.1- ¿Cómo dibujar las transversales de gravedad con regla y compás?

Para dibujar las transversales de gravedad de un triángulo ABC, usando sólo regla y compás, tienes que realizar los siguientes pasos en cada uno de los lados, en este caso trazaremos la transversal de gravedad que va desde el vértice C al lado AB;

1° Debes encontrar el punto medio del lado AB, el cual llamaremos D. Para esto, realiza el mismo procedimiento que aprendiste para dibujar las simetrales, entonces, utilizando el compás traza dos arcos, uno con centro en A y otro con centro en B, ambos con la misma abertura, suficiente para que los arcos se corten, luego, con una regla marca el punto medio;

 

 

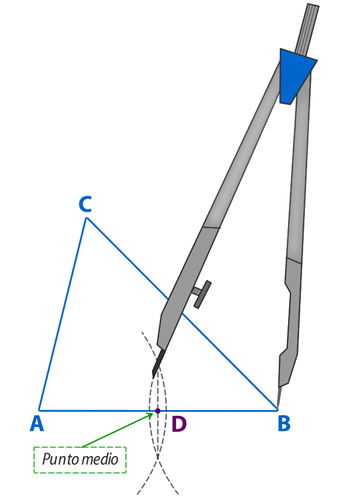
2° Une el vértice C con el punto D. El segmento AD corresponde a la transversal de gravedad del lado AB;

 

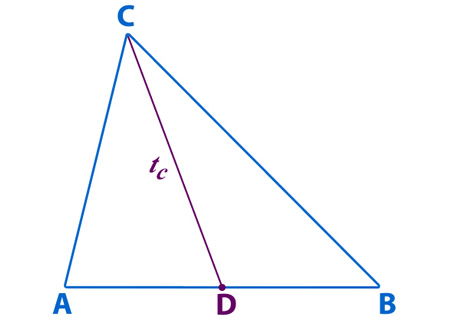
Para trazar las otras dos transversales de gravedad, debes seguir los mismos pasos, en los lados BC y CA.

 

Nota: En algunos países, a las transversales de gravedad también se les llama medianas, pero en Chile, el término mediana se utiliza para definir los segmentos que unen los puntos medios de cada lado del triángulo. Estos trazos dividen el triángulo, en 4 triángulos de iguales medidas.  Cada mediana es paralela al lado que no contiene sus extremos, y mide la mitad de ese lado del triángulo.

 

Ejemplo:

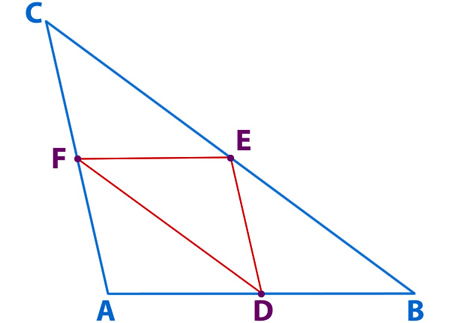
Tenemos un triángulo ABC, con los puntos medios D, E y F;

Las líneas rojas representan las medianas del triángulo.

Recuerda revisar también los otros elementos secundarios, alturas y bisectrices.