Elementos secundarios del triángulo: Alturas y bisectrices

1- Elementos del triángulo

Los elementos del triángulo son los que componen esta figura geométrica, los cuales se pueden definir como elementos primarios y secundarios.

Los elementos primarios son los vértices, lados y ángulos (interiores y exteriores).

Ejemplo elementos primarios:

 

 

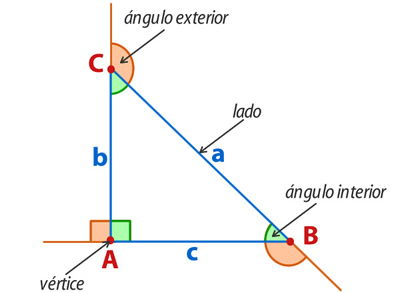
Como puedes ver, un triángulo tiene tres lados (dibujados en celeste), tres vértices (resaltados con un punto rojo), tres ángulos interiores (pintados en verde) y tres ángulos exteriores (pintados color naranjo).

Los elementos secundarios son las alturas, bisectrices, simetrales y transversales de gravedad, de los cuales detallaremos a continuación las alturas y bisectrices;

 

2- Alturas de un triángulo

Las alturas de un triángulo son aquellos segmentos que unen el vértice con su lado opuesto (o una prolongación de él) en forma perpendicular, es decir, son trazos que van desde el vértice y forman un ángulo de 90° con su lado opuesto. Cada triángulo como  tiene 3 vértices y 3 lados, siempre tendrá 3 alturas.

Las alturas se nombran con la letra h y un sub índice según la letra del vértice (ej.: h_a).

El punto donde se cortan  o coinciden las 3 alturas es un punto único llamado ortocentro y se nombra con la letra H. Las alturas en los triángulos acutángulos se interceptan en su interior, en los obtusángulos en el exterior y en los triángulos rectángulos 2 de sus alturas coinciden con los lados del triángulo y coinciden en el vértice del ángulo recto.

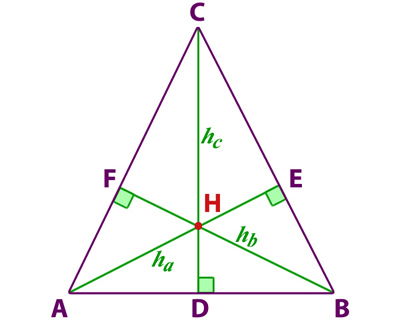
Ejemplo alturas en un triángulo acutángulo:

Sus medidas se denotan;                                     

AE = h_a

BF = h_b

CD = h_c

H = Ortocentro

 

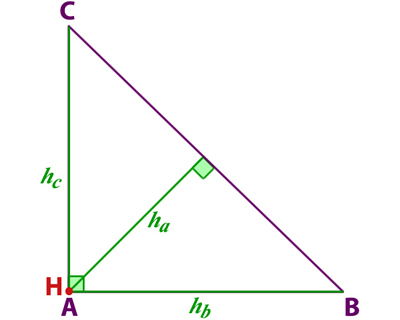
Ejemplo alturas en un triángulo rectángulo:

En este ejemplo marcamos con color verde las alturas sobre los catetos, para que las puedas identificar y el ortocentro (H) con un punto rojo, sobre el vértice A.

 

 

 

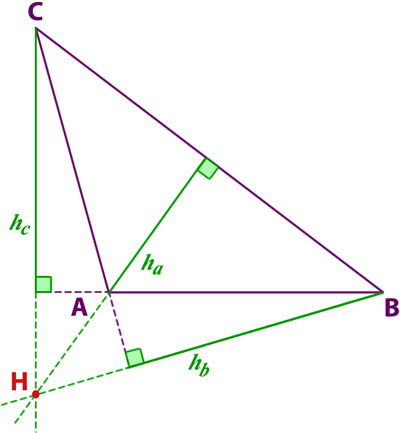
Ejemplo alturas en un triángulo obtusángulo:

Como puedes ver en este ejemplo, marcamos con línea punteada morada, la prolongación de los lados para marcar las alturas, y con línea punteada verde la prolongación de las alturas para encontrar el ortocentro (H).

 

2.1- ¿Cómo dibujar las alturas con regla y compás?

Si tenemos un triángulo ABC y quieres dibujar la altura desde el vértice A, tienes que realizar los siguientes pasos;

1° Traza una línea con una regla, alargando el lado BC en ambos sentidos, en esta línea dibuja con el compás apoyado en el vértice A (con una abertura cualquiera), dos puntos M (posición 1 en la gráfica) y N (posición 2 en la gráfica).

 

 

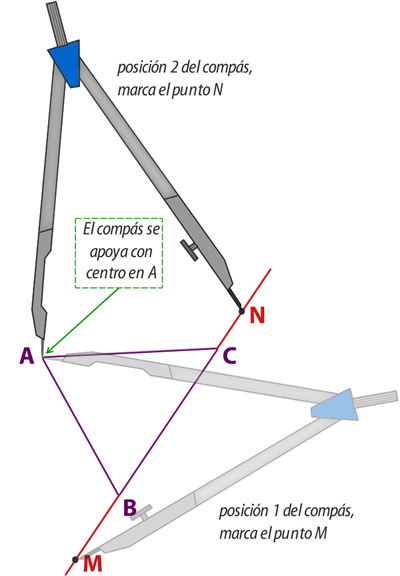
2° Con el compás apoyado en los puntos M, y luego N, dibuja dos arcos con la misma abertura, con un radio suficientemente para que éstos se corten en un punto, el cual llamaremos O.

 

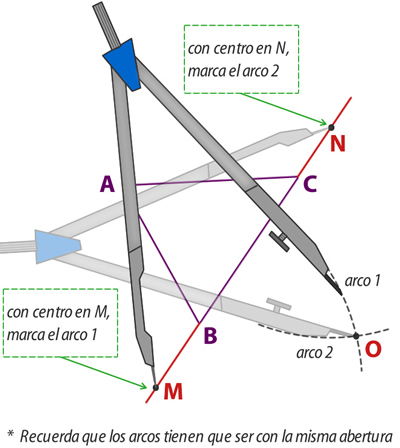
3° Con una regla, traza una recta desde el punto A hasta el punto O, marca el punto donde corte el lado BC, lo denominaremos D. Entonces, el segmento AD que obtuvimos, es la altura desde el vértice A. Si quieres encontrar las otras alturas, debes repetir los pasos anteriores sobre el lado correspondiente.

 

 

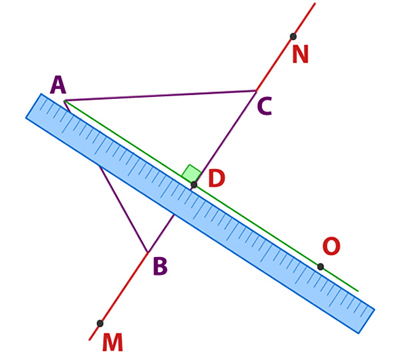
3- Bisectrices de un triángulo

Bisectriz es la recta interior que divide cada ángulo en dos ángulos iguales, donde los puntos de esta recta equidistan de los respectivos lados del ángulo. Cada triángulo tiene 3 bisectrices que se nombran con la letra b y un sub índice según el ángulo interior que divide (ej.: b_a).

El punto donde se cortan  las 3 bisectrices es un punto único llamado incentro y se nombra con la letra O, es el centro de la circunferencia inscrita en el triángulo.

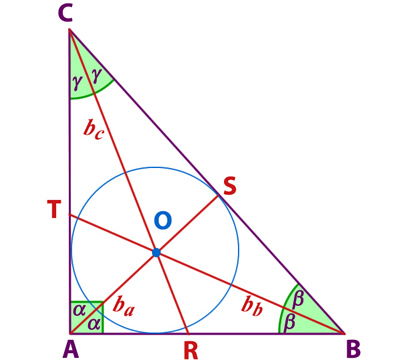
Ejemplo:

Sus medidas se denotan;                                     

AS = b_a

BT = b_b

CR = b_c

O = Incentro

 

3.1- ¿Cómo dibujar las bisectrices con regla y compás?

Si tenemos un triángulo ABC y quieres trazar la bisectriz desde el vértice B, tienes que realizar los siguientes pasos;

1° Traza una arco con centro en el vértice B, el compás puede tener cualquier abertura.

 

 

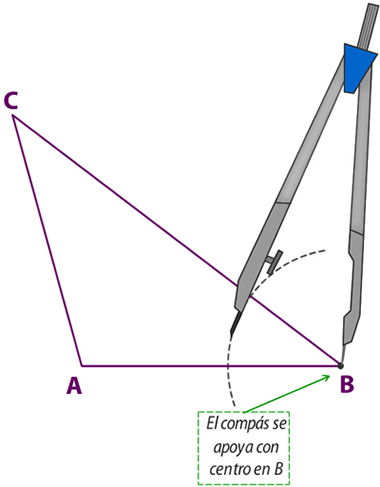
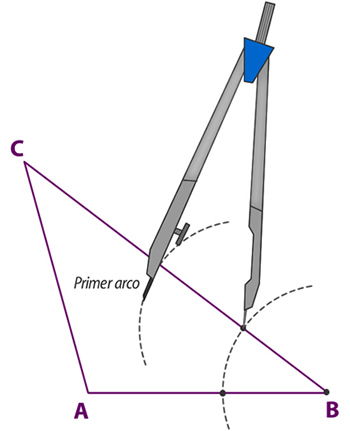
2° Traza dos arcos con la misma abertura que el paso anterior, utilizando como centros la intersección del primer arco con los lados del triángulo.

 

 

 

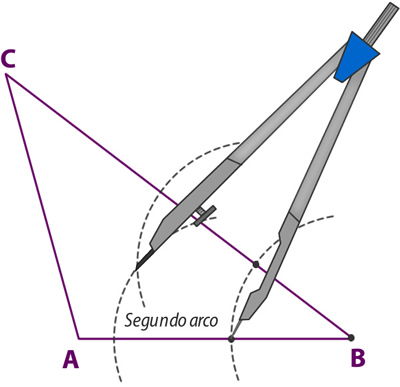
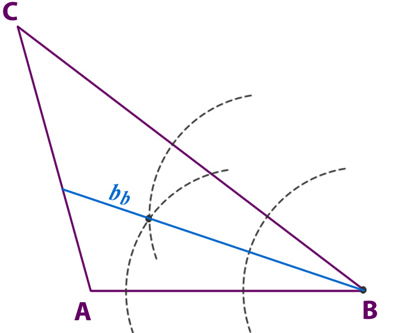
3° Traza una recta desde el vértice B y que pase por la intersección de los dos arcos que construiste en el paso anterior. Esta recta corresponde a la bisectriz b_b. Para trazar las otras dos bisectrices, repite los pasos anteriores pero desde los vértices A y C.

 

 

Revisa los otros dos elementos secundarios de un triángulo, simetrales y transversales de gravedad aquí.