Ecuación y sus partes

 

Una ecuación es una igualdad entre expresiones algebraicas que se cumple solamente para algunos valores de las letras.
 

Resolver una ecuación es encontrar el valor de la incógnita. Para esto debes aplicar algunas de las propiedades de las operaciones que has aprendido en cursos anteriores.

 

 

 

Miembros: son las expresiones que aparecen a cada lado del signo igual ( =)

 

 

Términos: son los monomios de cada miembro.

 

 

Incógnitas: Son las letras que aparecen en la ecuación.

 

 

 

Grado de la ecuación: es el mayor exponente con que figura la incógnita (una vez realizadas todas las operaciones).

 

 

Soluciones: son los valores que deben tener las incógnitas para que la igualdad entre los miembros sea cierta.

 

3- Resolver una ecuación

Recordemos que para resolver una ecuación se pueden aplicar las propiedades de la igualdad, realizando las operaciones inversas en ambos lados de la igualdad para despejar la incógnita.

Por ejemplo, si tenemos una ecuación de la forma: x + 4 = 20, utilizamos la operación inversa de la suma y restamos 4 en ambos miembros.
 

Veamos otro caso:

$5x + 13 = 3x + 21/ –13$          (Restamos 13 en ambos lados de la ecuación)
$5x + 13 – 13= 3x + 21 – 13$ 

                     $5x = 3x + 8/ –3x$   (Restamos -3x en ambos lados de la ecuación)

           $5x – 3x = 3x – 3x + 8$
              $2x = 8/÷2$                 (Dividimos por 2 en ambos lados de la ecuación)

                    $$\begin{gathered} \frac{2x}{2} = \frac{8}{2} \\ x = 4 \end{gathered}$$
             

 

4- Ejercicios resueltos

4.1- El triple de un número aumentado en 36 es igual a 75. ¿Cuál es el número?

Recordemos que el triple de un número se puede expresar como 3x y aumentado en 36 se relaciona con sumar 36. Entonces, la ecuación quedaría planteada de la siguiente manera:

 

$3x + 36 = 75$
 

Resolvemos la ecuación:

$$\begin{gathered} 3x + 36 = 75/ –36 \\ 3x + 36 – 36 = 75 – 36 \\ 3x = 39/÷3 \\ \frac{3x}{3}=\frac{39}{3} \\ x = 13 \end{gathered}$$

Respuesta: El número es 13.

4.2- ¿Cuál es la medida de los tres ángulos?

 

Para saber el valor de x, hay que considerar que la suma de los ángulos interiores de un triángulo es igual a 180°. Por lo tanto, la ecuación se puede modelar de la siguiente manera:

$3x + 8 + x + 34 + 2x + 18 = 180$

Reducimos términos semejantes y resolvemos la ecuación:
 

$$\begin{gathered} 3x + 8 + x + 34 + 2x + 18 = 180 \\ 6x + 60 = 180 / –60 \\ 6x + 60 – 60 = 180 – 60 \\ 6x =\hspace{0.17em}120/÷6 \\ \frac{6x}{6}=\frac{120}{6} \\ x \hspace{0.17em}= 20 \end{gathered}$$

Reemplazamos el valor de x, para saber el valor de los tres ángulos:

$$\begin{gathered} 3x + 8 \\ 3 \left(20\right) + 8 = 68° \end{gathered}$$
 

$$\begin{gathered} x + 34 \\ 20 + 34 = 54° \end{gathered}$$
 

$$\begin{gathered} 2x + 18 \\ 2 \left(20\right) + 18 = 58° \end{gathered}$$
 

Respuesta: Las medidas de los tres ángulos son 54°, 58° y 68°.

 

4.3- ¿Cuál es el valor de y en el siguiente caso?

 

 

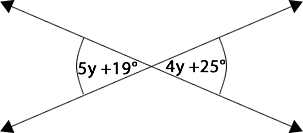
Hay que recordar que los ángulos opuestos por el vértice tienen la misma medida. Por lo tanto, la ecuación se puede modelar de la siguiente manera:
 

$$\begin{gathered} 5y + 19 = 4y +25/– 19 \\ 5y + 19 –19= 4y + 25 – 19 \\ 5y = 4y + 6/–4y \\ 5y – 4y= 4y – 4y +6 \\ y = 6 \end{gathered}$$

Respuesta: El valor de y es 6.

4.4- ¿Cuál es la medida del lado de un cuadrado si su perímetro es 2 652 cm?

Como el cuadrado tiene 4 lados de igual medida, un lado se puede denotar con una x y como son 4 lados corresponde a 4x. Entonces la ecuación se puede formular de la siguiente manera:

$$\begin{gathered} 4x =\hspace{0.17em}2 652/ ÷4 \\ \frac{4x}{4}=\hspace{0.17em}\frac{2 652}{4} \\ x=663 \end{gathered}$$

Respuesta: La medida del lado del cuadrado es 663 cm.

4.5- La entrada a una exposición de dinosaurios para un adulto cuesta el doble que la entrada de un niño. Si a una madre y su hijo de 9 años les cuesta $570 ambas entradas, ¿cuál es el valor de la entrada de un adulto y de un niño?

La ecuación se puede expresar de la siguiente manera:
Entrada de un niño: x
Entrada de un adulto: 2x

$$\begin{gathered} x + 2x = 570 \\ 3x = 570/÷3 \\ \frac{3x}{3} = \frac{570}{3} \\ x = 190 \end{gathered}$$

 

Ahora para saber el precio de la entrada de un adulto y un niño sustituimos el valor de x en las expresiones:
Entrada de un niño: x
$\$190$

Entrada de un adulto: 2x
$2\left(190\right) = \$380$

                                
Respuesta: La entrada de un niño cuesta $190 y la entrada de un adulto, $380.

 

4.6- Andrea compró 4 cajas de lápices de igual precio. Si pagó con un billete de $500 y recibió de vuelto $20. ¿Cuál es el precio de cada caja de lápices?

El valor de 4 cajas de lápices de igual precio se puede expresar como 4x y sabemos el vuelto que le dieron a Andrea. Entonces, la ecuación se puede plantear de la siguiente manera:
 

$$\begin{gathered} 4x + 20 = 500/– 20 \\ 4x + 20– 20= 500/– 20 \\ 4x = 480/÷4 \\ \frac{4x}{4}= \frac{480}{4} \\ x = 120 \end{gathered}$$

Respuesta: El precio de cada caja de lápices es $120.