¿Cómo resolver ecuaciones cuadráticas incompletas?

1- ¿Qué son las ecuaciones cuadráticas incompletas?

Se llama ecuaciones incompletas de segundo grado o cuadráticas, cuando la ecuación carece del término en $x$ o el término independiente, y se clasifican en ecuaciones cuadráticas incompletas puras (de la forma; $a{x}^2+c=0$) y mixtas (de la forma $a{x}^2+bx=0$), respectivamente.

 

1.1- ¿Cómo resolver ecuaciones cuadráticas incompletas puras?

Para resolver las ecuaciones cuadráticas incompletas puras de la forma $a{x}^2+c=0$, deberás despejar la incógnita. Para esto pasamos $\mathit{c}$ al 2° miembro, luego $\mathit{a}$ y por último el cuadrado de x,  como se muestra a continuación;

 

Entonces, las raíces (o soluciones) de una ecuación cuadrática incompleta pura son;

 

 

– Si $a$ y $c$ tienen el mismo signo, las raíces son imaginarias, por ser la raíz cuadrada de una cantidad negativa, y si tienen signo distinto las raíces son reales.

– También, se puede llegar al mismo resultado aplicando la fórmula general de la ecuación  cuadrática completa, teniendo presente que $b=0$, o sea, el término $bx$ es nulo, donde tenemos que;

Fórmula General;

 

 

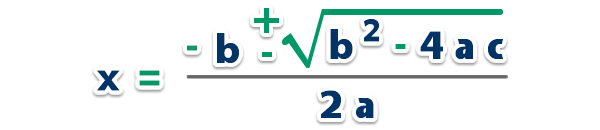
Si quitamos $b$, nos quedaría;

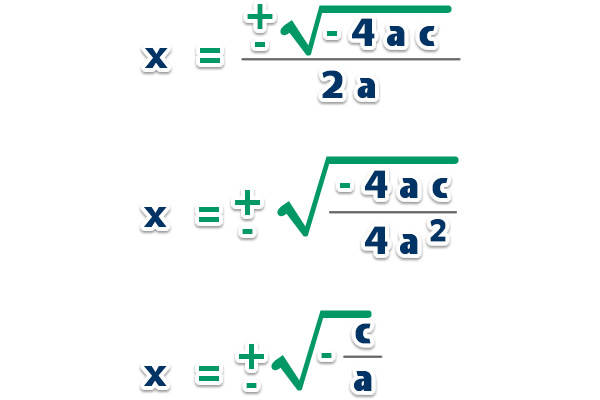
Ejemplos:

a) Resolver la ecuación $7x^2+14=0$.

Remplazamos los datos en la fórmula;

 

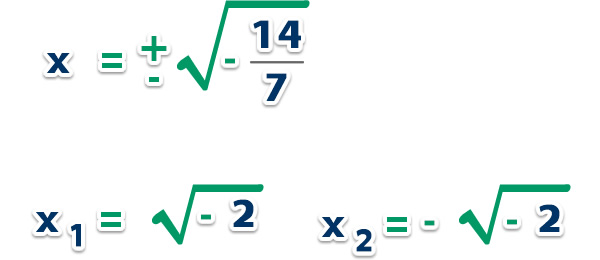
Respuesta: Las raíces de la ecuación son $\sqrt{–2}$ y  $–\sqrt{–2}$.  Las dos raíces son imaginarias

 

b) Resolver la ecuación (2x – 3) (2x + 3) – 135 = 0.

Primero resolvemos la ecuación, como hay un producto notable (suma por su diferencia) aplicamos la fórmula (a + (a – b) = a² – b²;   

 

 

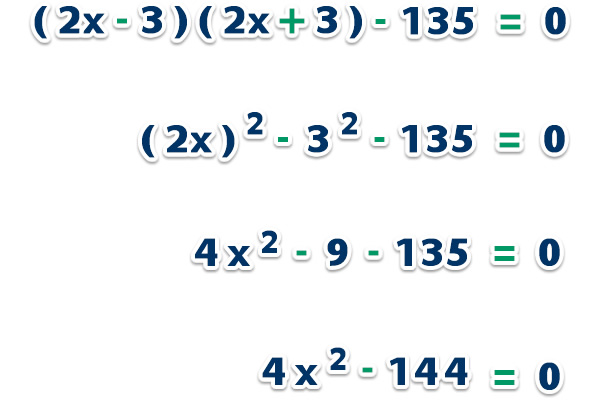
Ahora, reemplazamos en la fórmula;

 

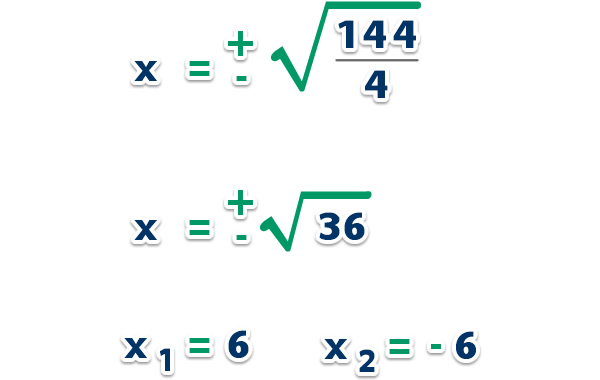
Respuesta: Las raíces son 6 y -6, las dos raíces son reales y racionales.

1.2- ¿Cómo resolver ecuaciones cuadráticas incompletas mixtas?

Para resolver las ecuaciones cuadráticas incompletas mixtas de la forma $a{x}^2+bx=0$, deberás factorizar la ecuación por $x$. Donde se tiene que;

 

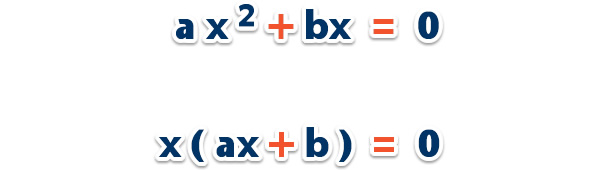
Igualando a cero ambos factores:

 

Recuerda que esto lo podemos realizar, ya que sabemos que si un producto es igual a cero, uno de sus multiplicandos o ambos, son iguales a cero.  

 

En las ecuaciones incompletas mixtas, siempre una raíz es cero, y la otra es el coeficiente del término en x con el signo cambiado partido por el coeficiente del término en x².

 

También, se puede llegar al mismo resultado aplicando la fórmula general de la ecuación cuadrática completa, teniendo presente que c = 0, o sea, el término independiente c es nulo, donde tenemos que;

La fórmula general es;

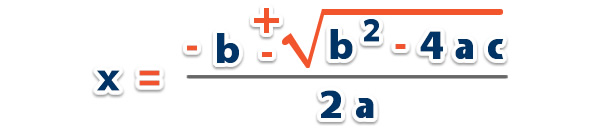
Si quitamos c, nos quedaría;

Y de aquí obtenemos;

 

 

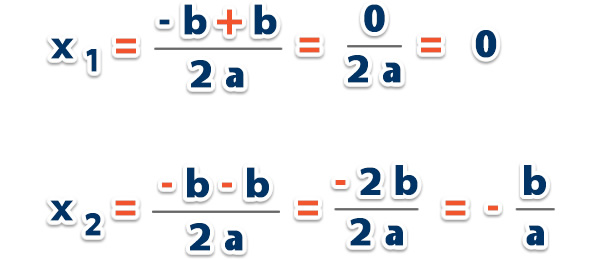
Ejemplos:

a) Resolver la ecuación $4x^2=–32x$

Ordenamos la ecuación;

 

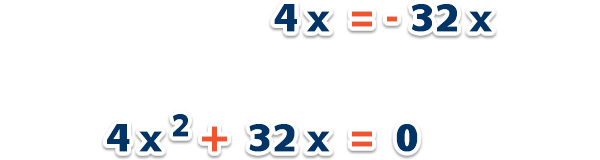
Reemplazamos en la fórmula;

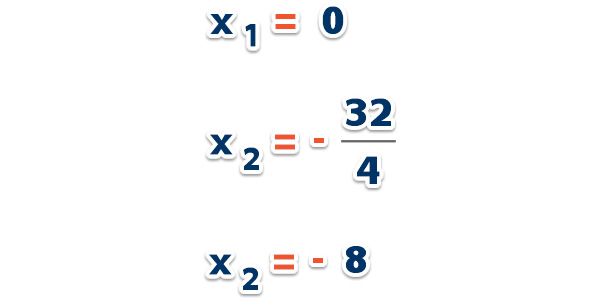
Respuesta: Las raíces son 0 y – 8.

 

b) Resolver la ecuación$\frac{x^2}{3}–\frac{x–9}{6}=\frac{3}{2}$       

 

Para resolver la ecuación hay que quitar los denominadores, para lo cual, tenemos que sacar el mínimo común múltiplo entre 3, 6 y 2, que es 6, y después transponemos los términos para igualar a 0;

 

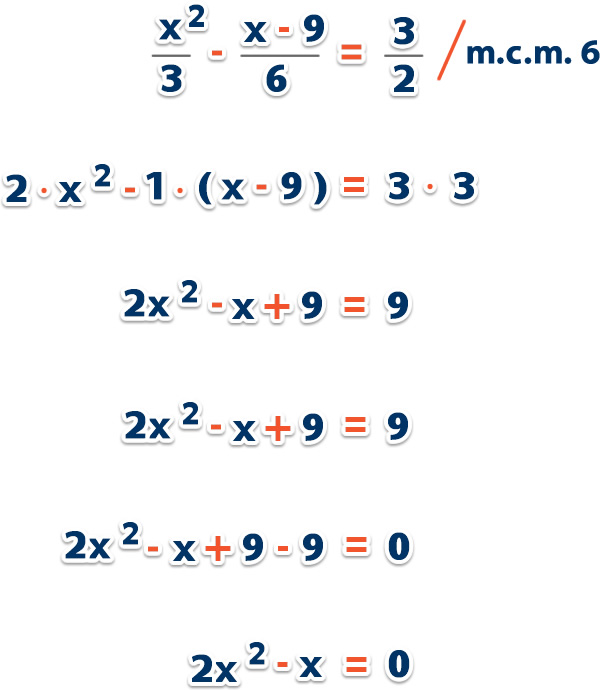
Reemplazamos en la fórmula;

 

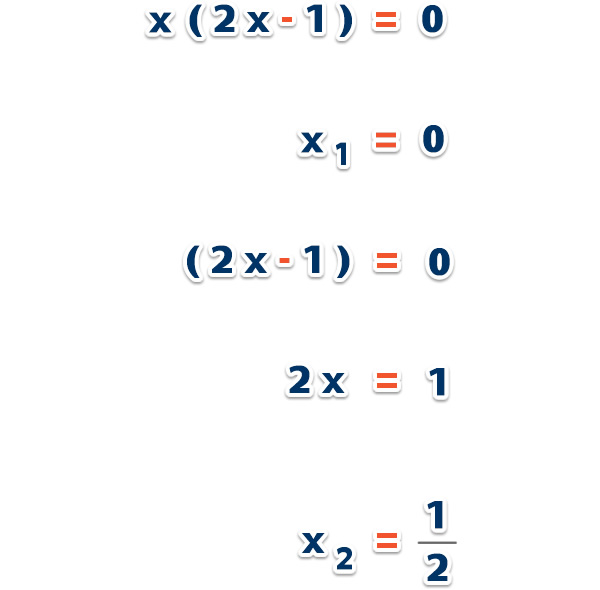
Respuesta: Las raíces son 0 y  $\frac{1}{2}$.