¿Cómo resolver una ecuación?

1- ¿Cómo se resuelven las ecuaciones?

Resolver una ecuación consiste en hallar los valores de la variable (por lo general "x") que hacen cierta la igualdad.

Para esto debes aplicar algunas de las propiedades de las operaciones (multiplicación, división, suma, resta, etc.) que aprendiste en cursos anteriores.

 

2- Términos semejantes

Se llaman términos semejantes a todos aquellos términos que tienen igual factor literal, es decir, la misma letra.

Reducir términos semejantes consiste en sumar o restar los coeficientes numéricos y conservar el factor literal común.

Ejemplos: 

a) 2x + 3x – 6 x + 4 x = 3 x

b) 5 x + 2 x + 3 y = 7 x + 3 y

 

Esto es muy importante en la resolución de ecuaciones ya que sólo se pueden sumar o restar términos que sean semejantes.

Además los términos semejantes se pueden reducir a un solo término, lo que facilita la resolución del problema. 

 

 

3- Ecuaciones y propiedades de la igualdad

Para despejar la incógnita se deben aplicar las propiedades de la igualdad.
– Si se suma o resta la misma cantidad en ambos miembros de la igualdad, esta se mantendrá.

Ejemplo:

$$\begin{gathered} 6 = 6 / +5 \\ 6 + 5 = 6 + 5 \\ 11 = 11 \end{gathered}$$                                 

– Si se multiplica o divide la misma cantidad en ambos miembros de la igualdad, esta se mantendrá.

Ejemplo:

$$\begin{gathered} 4 = 4 /\left(3\right) \\ 4\left(3\right) = 4\left(3\right) \\ 12 = 12 \end{gathered}$$

 

 

4- Recordemos diferentes tipos de ecuaciones
 

Ecuación de la forma x + a = b Se resta a en ambos lados de la ecuación. Ejemplo: $$\begin{gathered} x + 60 = 180 \\ x + 60 – 60 = 180 – 60 \\ x = 120 \end{gathered}$$

 

Ecuación de la forma x – a = b Se suma a en ambos lados de la ecuación. Ejemplo: $$\begin{gathered} x – 30 = 150 \\ x – 30 + 30 =150 + 30 \\ x = 180 \end{gathered}$$

 

Ecuación de la forma ax = b Dividimos a en ambos lados de la ecuación. Ejemplo: $$\begin{gathered} 8x = 240 \\ \frac{8x}{8}= \frac{240}{8} \\ x = 30 \end{gathered}$$

 

Ecuación de la forma $\frac{\mathbf{x}}{\mathbf{a}}\mathbf{=}\mathbf{ }\mathit{b}$ Multiplicamos por a en ambos lados de la ecuación. Ejemplo: $$\begin{gathered} \frac{x}{8} = 24 \\ 8 \left(\frac{x}{8}\right) = 24\left(8\right) \\ x = 192 \end{gathered}$$

 

Ecuación de la forma ax + b = c Primero restamos b en ambos lados de la ecuación. Luego, dividimos ambos lados por a. Ejemplo: $$\begin{gathered} 5x + 9 = 84 \\ 5x + 9 – 9 = 84 – 9 \\ 5x = 75 \\ \frac{x}{5} = \frac{75}{5} \\ x = 15 \end{gathered}$$

Resumen:

-Si un número está sumando a la incógnita, se debe restar en ambos lados ese mismo número.
– Si a la incógnita se le resta un número, se debe sumar en ambos lados ese mismo número.
– Si un número está multiplicando a la variable, se debe dividir en ambos lados de la igualdad ese mismo número.
– Si un número está dividiendo a la variable, se debe multiplicar en ambos lados de la igualdad ese mismo número.

 

 

5- Ecuaciones de la forma ax + b = cx + d

5.1- Representación en balanzas
Las ecuaciones se pueden representar como una balanza equilibrada, y los miembros de la igualdad están representados en los platillos derecho e izquierdo.  A continuación, se muestran algunos ejemplos:

Ejemplo: 2x + 2 = x + 4   
En el lado izquierdo de la balanza se representa la expresión 2x + 2 y en el plato derecho x + 4.

1- Para despejar la incógnita se quitan 2 unidades en ambos lados de la igualdad.

 

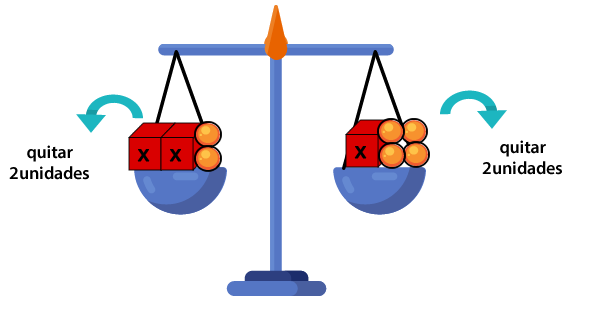
2x + 2 = x + 4 / -2
  2x + 2 -2 = x + 4 -2
       2x  = x + 2

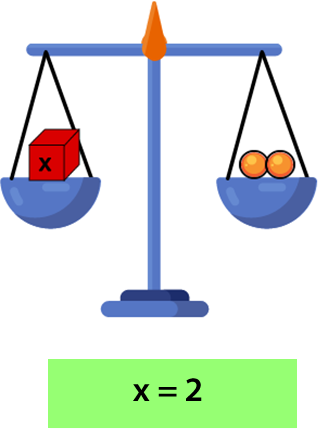
2- Luego, se quita una x en ambos lados de la igualdad.

2x  = x + 2  / -x
      2x – x = x -x + 2 
  x    =   2

3- Finalmente tenemos que el valor de la incógnita es igual a 2.

 

 

5.2- Resolver ecuaciones de la forma ax + b = cx + d

Para resolver estos tipos de ecuaciones debes seguir los pasos que se presentan a continuación:

Ejemplo:

$5x + 20 = 2x + 44$

Paso 1: Restar 20 en ambos lados de la igualdad.
 

$$\begin{gathered} 5x + 20 – 20 = 2x + 44 – 20 \\ 5x = 2x + 24 \end{gathered}$$

 

Paso 2: Restar 2x en ambos lados de la ecuación.

$$\begin{gathered} 5x – 2x = 2x – 2x + 24 \\ 3x = 24 \end{gathered}$$        

Paso 3: Dividir por 3 en ambos miembros de la ecuación:

$$\begin{gathered} \frac{3x}{3}= \frac{24}{3} \\ x = 8 \end{gathered}$$                                     

Paso 4: Comprueba que la solución esté correcta, sustituyendo x= 8 en la ecuación:

$$\begin{gathered} 5x + 20 = 2x + 44 \\ 5\left(8\right) + 20 = 2\left(8\right) +44 \\ 40 + 20 = 16 + 44 \\ 60 = 60 \end{gathered}$$

La igualdad se cumple, entonces la solución es correcta.

 

 

6- Ecuaciones con paréntesis

Cuando tenemos ecuaciones con paréntesis hay que aplicar la propiedad distributiva.

Ejemplo:

 

$3 (x + 2) = 4 + 2 (x + 2)$

$$\begin{gathered} 3 (x + 2) \to 3\left(x\right) + 3\left(2\right) \\ 3x + 6 \end{gathered}$$

 

$$\begin{gathered} 2 (x + 2) \to 2\left(x\right) + 2\left(4\right) \\ 2x + 8 \end{gathered}$$
 

Finalmente nos queda:

$3x + 6 = 2x + 8$
 

Aplicamos las propiedades de la igualdad para resolver la ecuación:
 

$$\begin{gathered} 3x + 6 = 2x + 8/ -6 \\ 3x + 6 -6 = 2x + 8 – 6 \\ 3x = 2x + 2/-2x \\ 3x – 2x = 2x – 2x + 2 \\ x = 2 \end{gathered}$$
 

A continuación, se remplaza x= 2 en la ecuación para verificar si está correcta:
 

$$\begin{gathered} 3 (x + 2) = 4 + 2 (x + 2) \\ 3 (2 + 2) = 4 + 2 (2 + 2) \\ 3 \left(4\right) = 4 + 2\left(4\right) \\ 12 = 4 + 8 \\ 12 = 12 \end{gathered}$$