Círculo y circunferencia: área, perímetro y longitud

3- Área del círculo

¿Cómo estimar el área de un círculo?

Estrategia 1: El área del círculo se puede estimar estableciendo una relación con el área de otra figura geométrica que hayas trabajado con anterioridad. En este caso, se aplicará la fórmula del área del cuadrado.

Ejemplo: El círculo está inscrito en un cuadrado de lado 10 cm. ¿Cuál es el área aproximada del círculo?
 

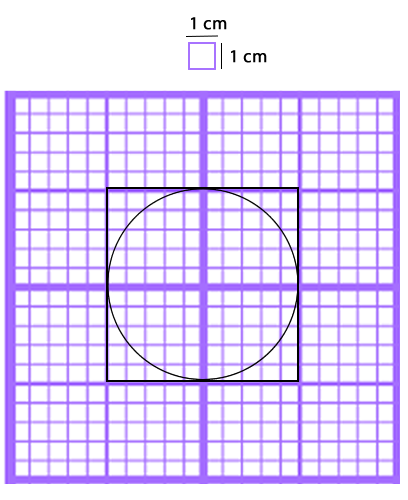
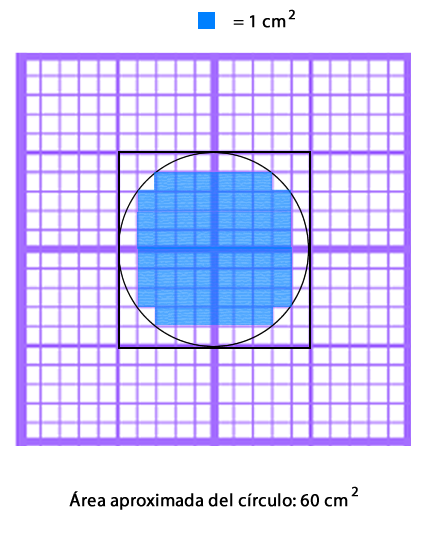
Para conocer el área aproximada del círculo, cuenta los cuadrados que están contenidos completamente en el interior del círculo. En este caso son 60 cuadrados.

 

A continuación, calcula el área del cuadrado.

 

 

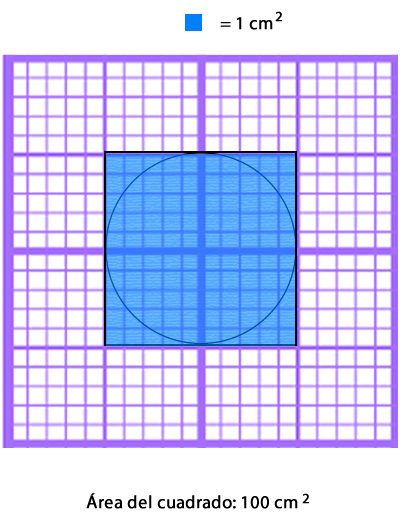
El cuadrado tiene en su interior 100 cuadrados, por lo tanto, su área es de 100 cm².

Entonces, el área estimada del círculo es un número mayor que 60 cm² y menor que 100 cm².

 

Estrategia 2:

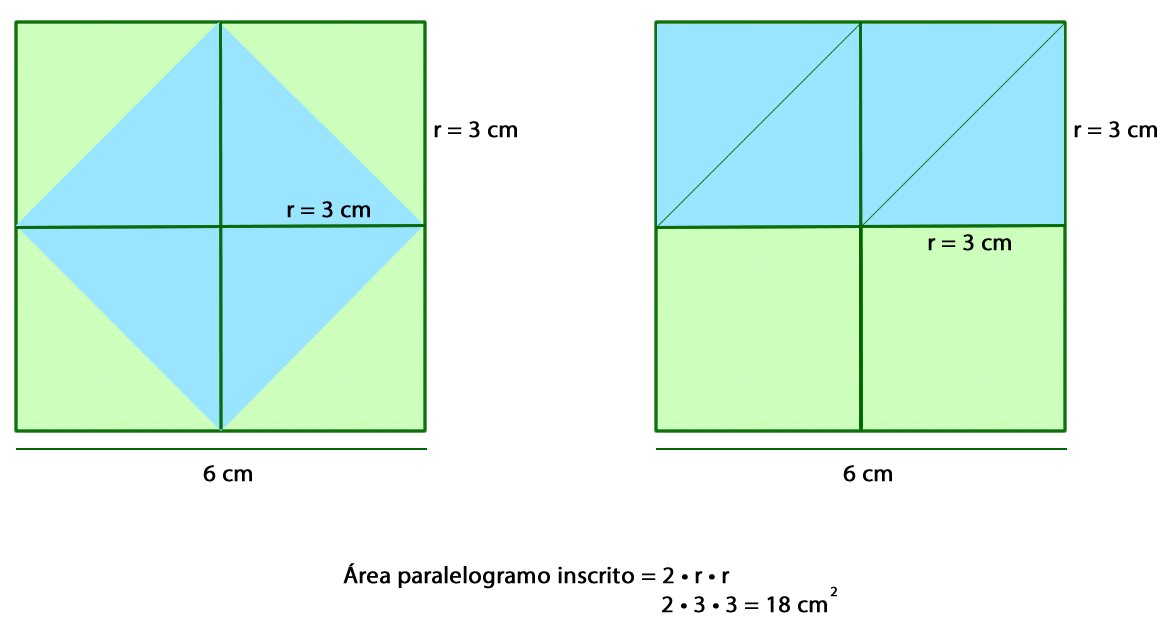
Estimar el área de un círculo en comparación con el cuadrado inscrito y circunscrito.
El radio del círculo es de 3 cm y el lado del cuadrado circunscrito mide 6 cm.

 

 

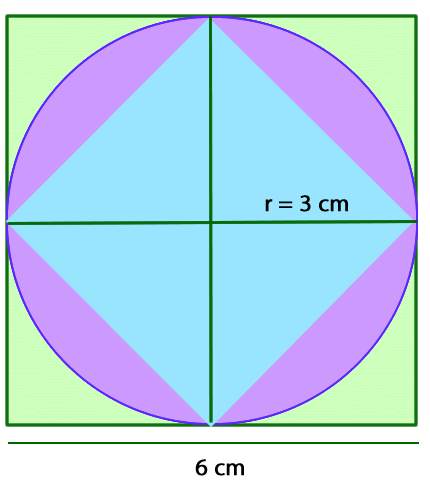
El área del cuadrado grande se puede expresar como 4r², ya que la medida del radio corresponde al lado de cada cuadrado pequeño.
 

El cuadrado grande tiene un área de 36 cm².

El área del paralelogramo celeste corresponde a la mitad del área del cuadrado grande, por lo tanto, su área se puede expresar como 2r².

 

 

Entonces, el área del círculo es mayor que 18 cm² y menor que 36 cm².
Si el área del cuadrado grande se relaciona con 4r²  y el del inscrito a 2r², entonces el área del círculo se puede aproximar a 3r².

 

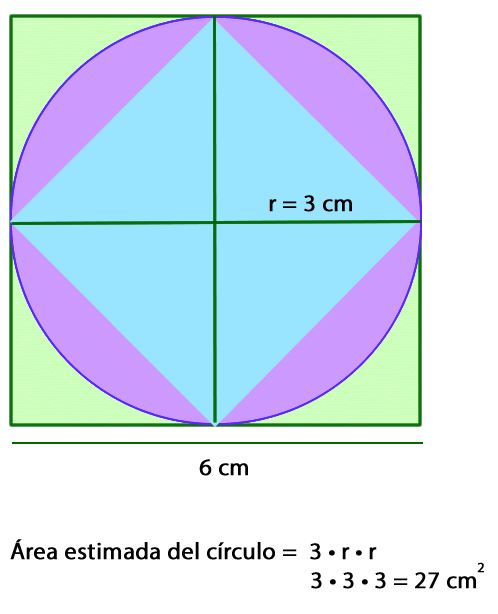
Por lo tanto, el área del círculo es aproximadamente 27 cm².

De acuerdo a la situación anterior, se puede establecer que el área del círculo se calcula multiplicando 3 por el radio elevado al cuadrado. Sin embargo, el valor más próximo es $\mathrm{\pi }$.

Entonces, el área del círculo es igual al valor de su radio elevado al cuadrado multiplicado por pi = p $·$ r².

 

 

Ejemplos:

1- Calcular el área de un círculo de radio 5 cm.

Para calcular el área de un círculo utilizamos la expresión:

$A =\hspace{0.17em}\mathrm{\pi } · {\mathrm{r}}^2$

Reemplazamos los valores en la fórmula:

$$\begin{gathered} \mathrm{A} \hspace{0.17em}=\hspace{0.17em}\mathrm{\pi } · {\mathrm{r}}^2 \\ \mathrm{A} \hspace{0.17em}= \mathrm{\pi } · 5^2 \\ \mathrm{A} \hspace{0.17em}= 25\mathrm{\pi } {\mathrm{cm}}^2 \end{gathered}$$

2- Calcular el área de un círculo de radio 9 cm. Considera $\mathrm{\pi } = 3,14$.

Reemplazamos los valores en la fórmula:
 

$$\begin{gathered} \mathrm{A} =\hspace{0.17em}\mathrm{\pi } · {\mathrm{r}}^2 \\ \mathrm{A} =\hspace{0.17em}3,14 ·9^2 \\ \mathrm{A} = 3,14 · 81 \\ \mathrm{A} = 254,34 {\mathrm{cm}}^2 \end{gathered}$$

3- Calcular el área de un círculo de radio 1,5 cm. Considera $\mathrm{\pi } =\hspace{0.17em}\hspace{0.17em}3,14.$

Reemplazamos los valores en la fórmula:

$$\begin{gathered} \mathrm{A} =\hspace{0.17em}\mathrm{\pi } · {\mathrm{r}}^2 \\ \mathrm{A} = 3,14 · 1,5^2 \\ \mathrm{A} = 3,14 ·2,25 \\ \mathrm{A} = 7,065 {\mathrm{cm}}^2 \end{gathered}$$

 

 

 

A continuación se presentan dos ejercicios del área del círculo:

1- Calcular el área de la zona achurada.

 

Paso 1: Calcular el área del círculo grande, su radio es de 17 cm.

$$\begin{gathered} \mathrm{\pi }· {\mathrm{r}}^2 \\ 3, 14 · {17}^2 \\ 3, 14 · 289 =\hspace{0.17em}\mathbf{907}\mathbf{,}\mathbf{46}\mathbf{ }{\mathbf{cm}}^{\mathbf{2}} \end{gathered}$$
Paso 2: Calcular el área del círculo de radio 10 cm.

$$\begin{gathered} \mathrm{\pi }· {\mathrm{r}}^2 \\ 3, 14 · {10}^2 \\ 3, 14 · 100 =\hspace{0.17em}\mathbf{314}\mathbf{ }{\mathbf{cm}}^{\mathbf{2}} \end{gathered}$$

Paso 3: Calcular el área del círculo de radio 7 cm.
$$\begin{gathered} \mathrm{\pi }· {\mathrm{r}}^2 \\ 3, 14 · 7^2 \\ 3, 14 · 49 =\hspace{0.17em}\mathbf{153}\mathbf{,}\mathbf{86}\mathbf{ }{\mathbf{cm}}^{\mathbf{2}} \end{gathered}$$

 

Paso 4: Restarle al círculo de radio 17 cm, el área de los círculos de radio 7cm y 10 cm.

$$\begin{gathered} 907, 46 – 314 – 153,86 \\ \mathbf{439}\mathbf{,}\mathbf{6}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}} \end{gathered}$$

 

2- Calcular el área de la zona achurada.

Paso 1: Calcular el área del círculo grande, su radio es de 5 cm. Luego, se divide el resultado por 2 (en la imagen se aprecia la mitad de un círculo).

$$\begin{gathered} \mathrm{\pi }· {\mathrm{r}}^2 \\ 3, 14 · 5^2 \\ 3, 14 · 25 =\hspace{0.17em}78,5 {\mathrm{cm}}^2 \end{gathered}$$

 

$78, 5 : 2 =\hspace{0.17em}\mathbf{39}\mathbf{,}\mathbf{25}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}}$

 

Paso 2: Calcular el área del círculo de diámetro 5 cm (su radio es la mitad = 2,5).  Luego, se divide por 2.

$$\begin{gathered} \mathrm{\pi }· {\mathrm{r}}^2 \\ 3, 14 · 2,5^2 \\ 3, 14 · 6,25 = \mathbf{19}\mathbf{,}\mathbf{625}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}} \end{gathered}$$

 

$19,625 : 2 =\hspace{0.17em}\mathbf{9}\mathbf{,}\mathbf{8125}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}}$

 

Paso 3: Calcular el área del círculo de diámetro 3 cm (su radio es la mitad = 1,5).  Luego, se divide por 2.

.$$\begin{gathered} \mathrm{\pi }· {\mathrm{r}}^2 \\ 3, 14 · 1,5^2 \\ 3, 14 · 2,25 = 7,065 c{m}^2 \end{gathered}$$

$7,065 : 2 =\hspace{0.17em}\mathbf{3}\mathbf{,}\mathbf{5325}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}}$

 

Paso 4: Calcular el área del círculo de diámetro 2 cm (su radio es la mitad = 1).  Luego, se divide por 2.

$$\begin{gathered} \mathrm{\pi }· {\mathrm{r}}^2 \\ 3, 14 · 1^2 \\ 3, 14 · 1 = 3,14 c{m}^2 \end{gathered}$$

 

$3,14 : 2 =\hspace{0.17em}\mathbf{1}\mathbf{,}\mathbf{57}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}}$

 

Paso 5: Restarle al área de círculo de radio 5, la mitad del área del círculo de radio 2,5.

$39,25 – 9,8125 =\hspace{0.17em}\mathbf{29}\mathbf{,}\mathbf{4375}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}}$

 

Paso 6: Sumarle a 29,4375 la mitad de las áreas de los círculos de diámetro 3 cm y 2 cm.

 

$29,4375 + 3,5325 + 1,57 = \mathbf{34}\mathbf{,}\mathbf{54}\mathbf{ }\mathit{c}{\mathit{m}}^{\mathbf{2}}$

 

5- Resolución de problemas

Situación 1:

Nuestro planeta tiene una forma casi esférica achatada por los polos y más ancha en su zona ecuatorial. A esta particular forma se le denomina geoide.

La Tierra es representada en globos terráqueos y planisferios, ambos están rodeados de líneas imaginarias muy finas que van de un polo al otro polo (de Norte a Sur), llamadas meridianos, y otras que son circunferencias menores llamadas paralelos que van de Este a Oeste.

Existen 90 paralelos hacia el norte e igual número hacia el Sur. Los paralelos más importantes son cuatro, en el hemisferio Norte se ubican el Trópico de Cáncer y el Círculo Polar Ártico, en el hemisferio Sur tenemos el Trópico de Capricornio y el Círculo Polar Antártico.
 

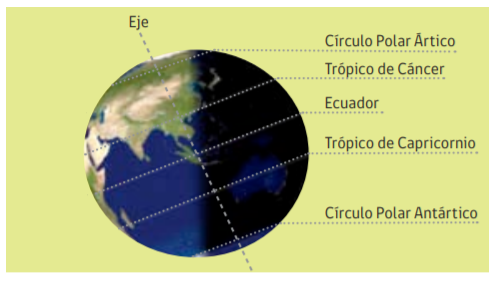
De acuerdo a los datos sobre el planeta Tierra, el radio ecuatorial es de 6 378 km y el radio polar es de 6 357 km.

 

1. Con relación a los datos presentados. Calcula la medida de la línea del Ecuador.

Recuerda que para calcular el perímetro se puede multiplicar el valor del diámetro por π. Se considerará π = 3,14

$$\begin{gathered} P =\hspace{0.17em}d · \mathrm{\pi } \\ \mathrm{P} =\hspace{0.17em}12 756 · 3,14 \\ \mathrm{P} = 40 053,84 \end{gathered}$$

Respuesta: La medida de la línea del Ecuador es de 40 053,84 km aproximadamente.

Situación 2:

El riego por pivote central capta el agua desde un embalse, río o lago y a través de cañerías se transporta el agua hasta la torre central.  El agua es distribuida a los aspersores que riegan el terreno formando patrones circulares como se muestra en la imagen.

 

 

1- Si en un terreno se utiliza el método de riego por pivote como se representa en la imagen. ¿Cuál es la superficie del terreno que se regó?

 

 

 

En este caso, se calcula el área del círculo empleando la fórmula, considera $\mathrm{\pi }$ = 3,14

$$\begin{gathered} A =\hspace{0.17em}\mathrm{\pi }·{\mathrm{r}}^2 \\ \mathrm{A} = 3,14 · {100}^2 \\ \mathrm{A} = 3,14 · 10 000 \\ \mathrm{A} = 31 400 \end{gathered}$$

Respuesta: La s