1- El círculo
Es la región comprendida por todos los puntos de la circunferencia.
|
Sector Circular |
Segmento Circular |
Corona Circular |
Trapecio Circular |
|
|
|
|
|
La circunferencia es una línea curva y cerrada que se caracteriza en que todos sus puntos equidistan (están a la misma distancia) de otro punto llamado centro. Puede identificarse como el contorno de un círculo.
La distancia entre el centro y cualquier punto de la circunferencia es conocida como radio (r).
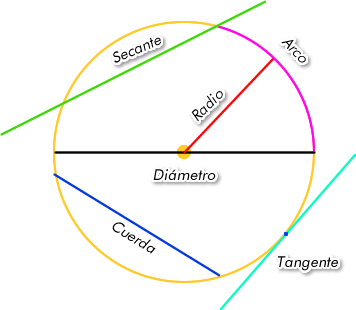
– Radio (r): segmento que une el centro con un punto cualquiera de la circunferencia. También se conoce como radio la longitud de estos segmentos.
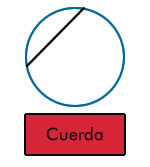
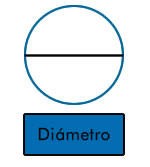
– Diámetro (d): cuerda que pasa por el centro de la circunferencia y equivale a dos radios. Por lo tanto, el diámetro = 2 · radio. Es la cuerda de mayor longitud y divide a la circunferencia en dos semicircunferencias congruentes.
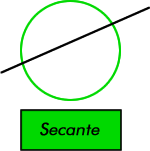
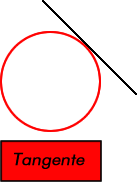
Para poder medir los ángulos dentro de la circunferencia utilizamos los grados. Un grado corresponde a la parte de una circunferencia. Es decir, se divide el perímetro del círculo en 360 partes iguales, en donde a cada parte le corresponde 1 grado.
Por ejemplo:
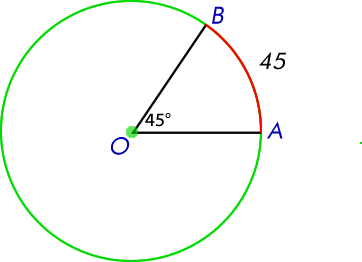
El arco corresponde a 45 de las 360 partes en la que se dividió la circunferencia, por lo que el ángulo mide 45 grados. Además, podemos decir que el arco correspondiente mide 45 grados , haciendo una equivalencia con el ángulo.
De manera general:
parte de la circunferencia
Importante: En la circunferencia, el valor del arco se lee siempre en sentido antihorario.
3- Ángulos de la circunferencia
Algunos ángulos en la circunferencia son:
3.1- Ángulo del centro: tiene su vértice en el centro de la circunferencia y sus lados son los radios de esta.
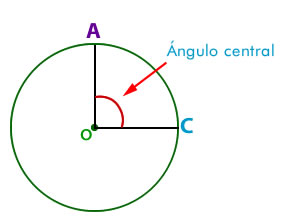
4.1-Ángulo del centro
El ángulo del centro es equivalente a la medida del arco que subtiende.
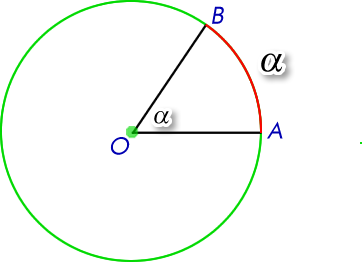
Por ejemplo:
Si formamos un ángulo de 70 grados a partir de dos radios desde el centro (En este caso OA y OB), la medida angular del arco correspondiente (AB) también es de 70.
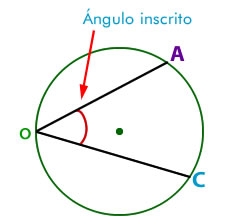
4.2- Ángulo inscrito
La medida del ángulo del centro es igual a la mitad del ángulo del centro. También es igual a la mitad de la medida angular del arco correspondiente.
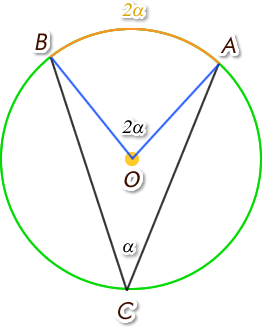
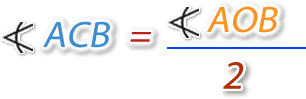
De esta propiedad, podemos deducir que:
a) si dos o más ángulos inscritos subtienden un mismo arco (en este caso, x), sus medidas son iguales.
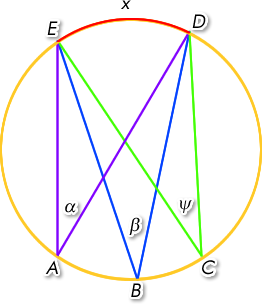
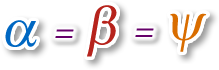
b) Si un ángulo inscrito tiene le corresponde como arco la mitad de la circunferencia, entonces ese ángulo es recto (90 grados).
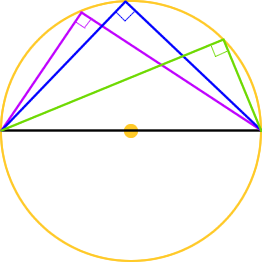
Esto es porque la circunferencia puede representarse en grados sexagesimales, en donde su totalidad corresponde a 360 grados. Si tomamos como arco la mitad de la circunferencia, estaríamos trabajando con (360/2), que es igual a 180 grados.
Como el ángulo inscrito es igual a la mitad de la medida angular de su arco, entonces el ángulo equivale a (180/2) = 90 grados.