1- Introducción
En esta clase vamos a trabajar con la esfera, determinaremos las fórmulas de área y volumen de ellas y trabajaremos la esfera como un sólido de revolución, esto es, un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que es contenida en su mismo plano. En principio, cualquier cuerpo con simetría axial o cilíndrica es un sólido de revolución.
Se denomina sólido de revolución o volumen de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no interceptarse, dicha recta se denomina eje de revolución.
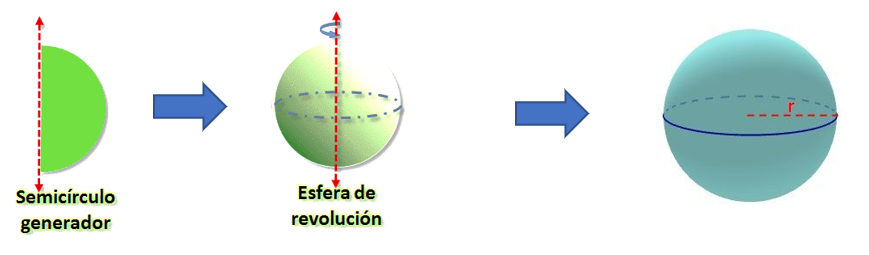
La esfera, como sólido de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro. Usualmente, se utiliza la palabra “bola”, para describir al cuerpo delimitado por una esfera.
2- Elementos de una esfera
La esfera es el conjunto de puntos del espacio tridimensional que equidistan de un punto definido como el centro de la esfera. O lo que es lo mismo, es la figura geométrica descrita por un semicírculo al girar sobre su diámetro.
Un círculo es la superficie que existe dentro de una circunferencia.
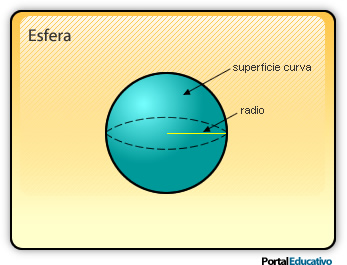
El radio es la distancia del centro a cualquier punto de superficie.
El diámetro es la distancia de un punto a otro de la superficie, pasando por el centro de la esfera.
El centro corresponde al punto central en el interior de la esfera, equidistante de todos los puntos de la superficie.
Los polos de la esfera son los puntos de la superficie de unión con el eje de rotación.
El eje es el diámetro del círculo sobre el cual gira.
La superficie curva es la que genera la rotación del semicírculo.
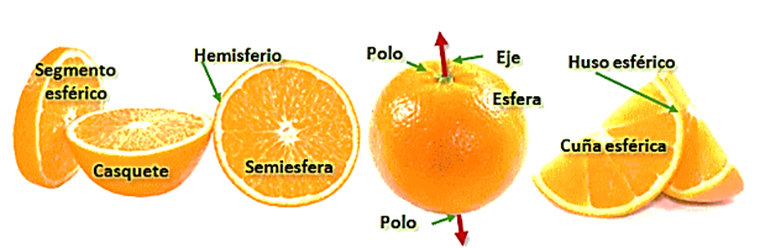
El hemisferio corresponde a cada una de las partes en queda dividida la superficie por un plano que pasa por el centro de ella.
El huso esférico es parte de la superficie de una esfera comprendida entre dos planos que se cortan en el diámetro de ella.
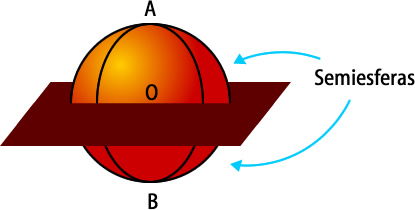
Las semiesferas son cada una de las dos mitades de una esfera dividida por un plano que pasa por su centro.
El segmento esférico es una parte de la esfera comprendida entre dos planos secantes.
El casquete esférico corresponde a cada una de las partes de la esfera al ser cortadas por un plano secante.
La cuña esférica es la parte de una esfera comprendida entre dos planos que se intersecan en el diámetro de ella
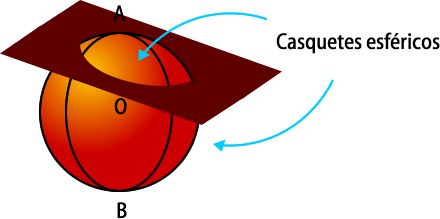
3- Área de la esfera
El área de superficie de una esfera es igual al área lateral de superficie de un cilindro que tiene el mismo radio de la esfera y una altura de longitud del diámetro de la esfera.
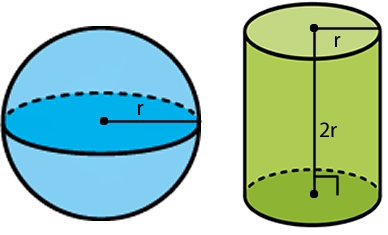
El área lateral del cilindro es donde , luego:
Área lateral del cilindro es .
Por lo tanto, el área de una esfera con radio es
Ejemplos:
1. Determina el área de una esfera de radio 5 cm.
Área = .
2. El diámetro del planeta Marte mide 6.795 kilómetros, ¿cuánto mide su superficie?
Aquí, el radio del planeta Marte es: .
Luego la superficie es:
4- Volumen de la esfera
Para encontrar el volumen de las esferas, podemos utilizar las pirámides.
Imaginemos una pirámide con su base en la superficie de la esfera y su vértice superior como el centro de la esfera.
El radio de la esfera puede ser la altura de la pirámide.
La pirámide ocupa una porción del volumen de la esfera. Si podemos llenar la esfera con pirámides como esta, conoceríamos el volumen de la esfera. Sería igual a los volúmenes de todas las pirámides juntas.
¿Cuántas pirámides haría falta para llenar una esfera?

Eso depende del área de superficie de la esfera. Podemos combinar el área de superficie de una esfera con la fórmula de volumen de una pirámide para calcular el volumen de todas las pirámides dentro de la esfera.
Así: , donde representa el área de la base de una pirámide.
Ahora, el área de la esfera es igual al área de las bases de todas las pirámides.
La altura de la pirámide es igual al radio de la esfera, por lo que debemos sustituir por . Luego:
Si simplificamos la fórmula, tenemos:
Ejemplos:
1. Calcula el volumen en metros cúbicos de una esfera cuyo diámetro mide 100 centímetros.
Aquí el radio es:
Luego:
2. Javiera tiene una botella de perfume en forma de esfera. El diámetro de la botella es . ¿Cuánto perfume quedo en la botella de Javiera si la botella está medio llena?
Aquí debemos calcular la mitad de la capacidad de la botella de perfume, esto es:
Debemos fijarnos que nos dan el diámetro, luego el radio es 3:
Recuerda que: es un número irracional, cuyo valor truncado con 15 decimales es:
y por lo general, se aproxima a

