Área y perímetro de sector y segmento circular

Área y perímetro de sector y segmento circular

El círculo corresponde al lugar geométrico formado por todos los puntos de la circunferencia y sus puntos interiores.

Las regiones del círculo son:

 

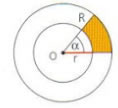
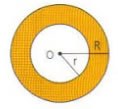
Sector Circular	Segmento Circular	Corona Circular	Trapecio Circular

 

En las regiones circulares, es necesario conocer la longitud del arco que delimita una parte de la región.

 

 

1- Longitud del Arco de una circunferencia

Para calcular la longitud de un arco de circunferencia se utiliza la siguiente relación:

 

 

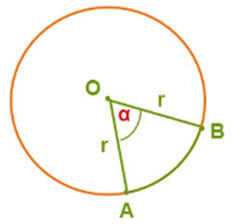
$L\left(\widehat{AB}\right)=\frac{2\mathrm{\pi }·\mathrm{r}·\mathrm{\alpha }}{360°}$ Dónde: r : radio de la circunferencia α : ángulo del centro que subtiende al arco AB

 

 

 

2- Perímetro del Sector Circular

El perímetro de cualquier figura geométrica se determina como la suma de todos los lados que rodean cierta región. En el caso del perímetro del sector circular, los segmentos que delimitan esta región son los dos radios y el arco subtendido por el ángulo central del sector circular.

Es decir:

$P_{\left(sector circular\right)}=2·r+L\left(\widehat{AB}\right)$

 

Dónde:                                                                                                                     

P : Perímetro del sector circular.

r  : radio del círculo.

$L\left(\widehat{AB}\right)$: Longitud del arco subtendido por los dos radios.

 

 

 

Ejemplo 1:
Determina el perímetro del siguiente sector circular:

 

 

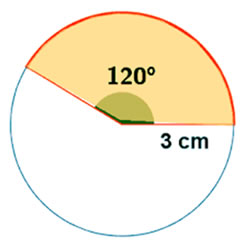
Para determinar el perímetro del sector circular se debe conocer la longitud del arco de la figura, el cual está marcado en rojo. Reemplazando el radio y el valor del ángulo:

 

 

$$\begin{gathered} L\left(\widehat{AB}\right)=\frac{2\pi ·r·\alpha }{360°} \\ L\left(\widehat{AB}\right)=\frac{2\pi ·3\left[cm\right]·120°}{360°} \\ L\left(\widehat{AB}\right)=\frac{2\pi \left[cm\right]·360°}{360°} \\ L\left(\widehat{AB}\right)=2\pi \left[cm\right] \end{gathered}$$

 

Luego se reemplazan los valores en la fórmula de perímetro del sector circular.

 

$$\begin{gathered} P_{(sector circular)}=2·r+L\left(\widehat{AB}\right) \\ {P}_{(sector circular)}=2·3\left[cm\right]+2\pi \left[cm\right] \\ {P}_{(sector circular)}=6\left[cm\right]+2\pi \left[cm\right] \end{gathered}$$

 

Debido a que el valor de π es infinito, se debe dejar expresado el resultado, ya que algebraicamente no se pueden sumar expresiones con factor literal diferente, en palabras simples no se pueden sumar “peras con manzanas”.

 

 

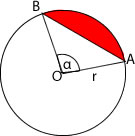
3- Perímetro del Segmento Circular

El perímetro de cualquier figura geométrica se determina como la suma de todos los lados que rodean cierta región. En el caso del perímetro del segmento circular, los segmentos que delimitan esta región son una cuerda del círculo y el arco subtendido por el ángulo central del sector circular.

Es decir:

 

$P_{\left(segmento circular\right)}=L\left(\widehat{AB}\right)+m\left(\overline{AB}\right)$

 Dónde:

P : Perímetro del segmento circular.

$m\left(\overline{AB}\right)$: Segmento que une los puntos del arco.

$L\left(\widehat{AB}\right)$: Longitud del arco subtendido por los dos radios.

 

Ejemplo 2:
Determina el perímetro del siguiente segmento circular:

 

 

Para determinar el perímetro del segmento circular se debe conocer la longitud del arco de la figura y el valor de la cuerda AB. Reemplazando el radio y el valor del ángulo (ángulo recto = 90°)

 

A) Cálculo de la longitud del arco.

 

$$\begin{gathered} L\left(\widehat{AB}\right)=\frac{2\pi ·r·\alpha }{360°} \\ L\left(\widehat{AB}\right)=\frac{2\pi ·5\left[cm\right]·90°}{360°} \\ L\left(\widehat{AB}\right)=\frac{2\pi \left[cm\right]·450° }{360°} \\ L\left(\widehat{AB}\right)=\frac{900\pi \left[cm\right]}{360}=\frac{10}{4}\pi \left[cm\right] \end{gathered}$$

 

 

B) Cálculo del segmento AB.

La cuerda AB es la hipotenusa del triángulo formado en la figura, la cual se calcula con el Teorema de Pitágoras.

 

$a^2+b^2=c^2$

 

Luego se reemplazan los valores de los catetos a y b (5 cm)

 

$$\begin{gathered} 5^2+5^2=c^2 \\ 50=c^2 \\ c=\sqrt{50}cm \end{gathered}$$

 

Es decir la cuerda AB, tiene un valor de $\sqrt{50} cm.$

 

C) Cálculo del perímetro del segmento circular.

Reemplazando en la fórmula:

 

$$\begin{gathered} P_{(segmento circular)}=L\left(\widehat{AB}\right)+m\left(\overline{AB}\right) \\ {P}_{(segmento circular)}=\frac{10}{4}\pi \left[cm\right]+\sqrt{50} cm \end{gathered}$$

 

Debido a que el valor de π es infinito, se debe dejar expresado el resultado, ya que algebraicamente no se pueden sumar expresiones con factor literal diferente, en palabras simples no se pueden sumar “peras con manzanas”.

 

 

4- Área del sector circular

El área de cualquier figura geométrica corresponde a la región que está delimitada por ciertos elementos. En el caso de un sector circular esto corresponde a toda la región que se encuentra entre dos radios y un arco subtendido por estos dos radios.

 

 

La relación matemática en este caso es:

$A_{sector circular}= \pi ·r^2·\frac{\alpha }{360°}$

 

Ejemplo 3:

Determina el área del sector circular de la figura.

 

 

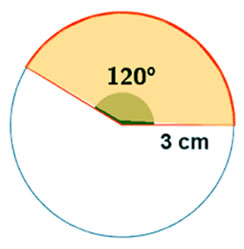
Reemplazando en la fórmula se obtiene que:

$$\begin{gathered} A_{sector circular}= \pi ·r^2·\frac{\alpha }{360°} \\ {A}_{sector circular}= \pi ·(3 \left[cm\right]{)}^2·\frac{120°}{360°} \\ {A}_{sector circular}= \pi ·9{\left[cm\right]}^2·\frac{1}{3} \\ {A}_{sector circular}= 3\pi {\left[cm\right]}^2 \end{gathered}$$

 

 

5- Área del segmento circular

En el caso de un segmento circular esto corresponde a toda la región que se encuentra entre dos radios y una cuerda de la circunferencia. 

 

 

La relación matemática en este caso es:

 

$A_{segmento circular}= A_{sector circular} –A_{triángulo}$

 

Ejemplo 4:

Determina el área del segmento circular de la figura.

 

 

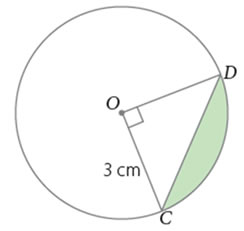
 Se necesita reemplazar en la fórmula el área del sector circular y el área del triángulo formado.

 

A) Área del sector circular:

 

$$\begin{gathered} A_{sector circular}= \pi ·r^2·\frac{\alpha }{360°} \\ {A}_{sector circular}= \pi ·(3\left[cm\right]{)}^2·\frac{90°}{360°} \\ {A}_{sector circular}= \pi ·9{\left[cm\right]}^2·\frac{1}{4} \\ {A}_{sector circular}= \frac{9\mathrm{\pi }}{4} {\left[cm\right]}^2 \end{gathered}$$

 

B) Área del triángulo:

Asumiendo que la base del triángulo corresponde a un radio ( en rojo)  y que la altura también corresponde a un radio ( en verde), se obtiene:

 

 

 

$$\begin{gathered} Áre{a}_{triángulo}=\frac{base·altura}{2} \\ Áre{a}_{triángulo}=\frac{3 \left[cm\right]·3\left[cm\right]}{2} \\ Áre{a}_{triángulo}=\frac{9 {\left[cm\right]}^2}{2} \end{gathered}$$

 

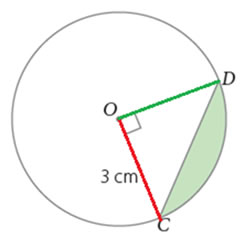
C) Área del segmento circular:

Reemplazando:

$$\begin{gathered} A_{segmento circular}= A_{sector circular} –A_{triángulo} \\ {A}_{segmento circular}=\frac{ 9\pi }{4}{\left[cm\right]}^2–\frac{9}{2}{\left[cm\right]}^2 \\ {A}_{segmento circular}=\left(\frac{9\mathrm{\pi }–18}{4}\right){\left[cm\right]}^2 \end{gathered}$$