Ángulos en un triángulo y un cuadrilátero

1- Ángulos en un triángulo

1.1- Actividades iniciales
Antes de comenzar recordemos que el triángulo es un polígono que tiene 3 lados, 3 vértices y 3 ángulos interiores.

Actividad 1
1- Dibuja un triángulo cualquiera y recórtalo.

 

 

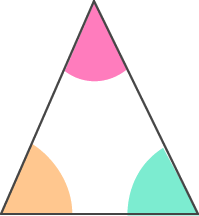
2- Recorta sus ángulos interiores.  

3- Dibuja en una hoja una recta y ubica los ángulos uno al lado del otro como se muestra en la figura. Luego responde, ¿qué medida tiene el ángulo que se forma?

 

 

Actividad 2
1- Dibujo un triángulo cualquiera.
2- Mide los ángulos interiores del triángulo con un transportador.
3- Suma las medidas de los ángulos, ¿qué resultado obtuviste?

 

1.2- Medida de ángulos interiores de un triángulo

Como pudiste ver en las actividades anteriores, la suma de los ángulos interiores de cualquier triángulo es 180°.

A continuación, lo verificaremos analizando el siguiente caso:

En la siguiente imagen se muestra el triángulo ABC:

 

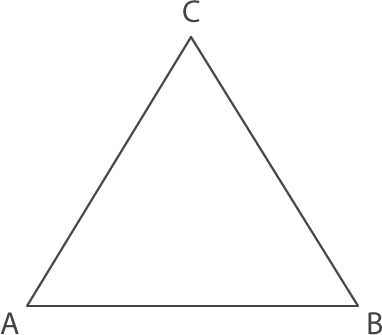
Al prolongar los lados AC y BC y trazar un segmento paralelo a AB se forman los siguientes ángulos:

 

 

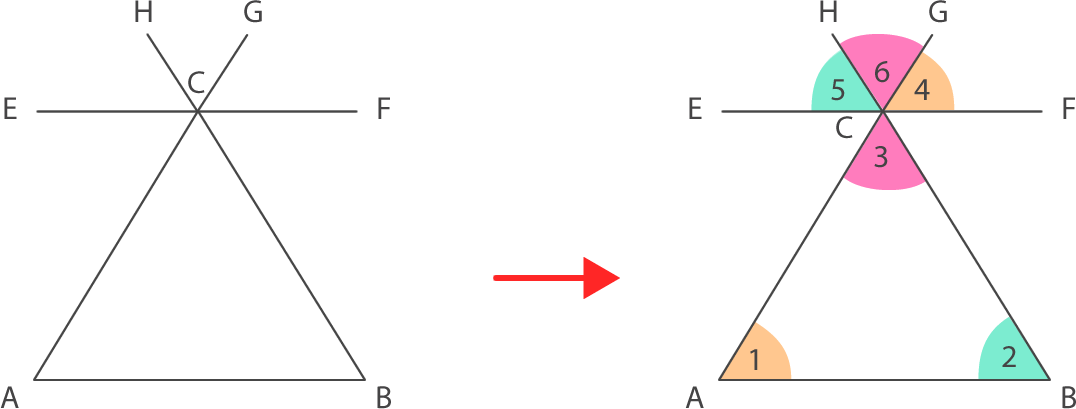
Ahora aplicaremos los conocimientos previos sobre los ángulos que se forman en rectas paralelas cortadas por una transversal.
 

 

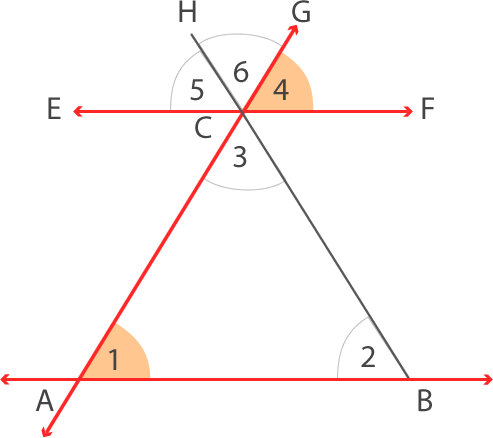
Los ángulos 1 y 4 son correspondientes, por lo tanto, tienen la misma medida.

 

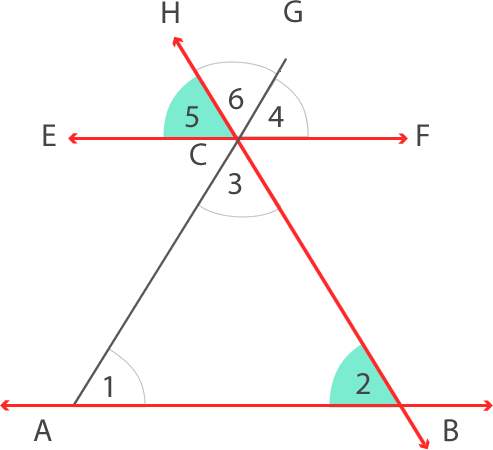
Los ángulos 2 y 5 también son correspondientes, por lo que tienen la misma medida.

 

 

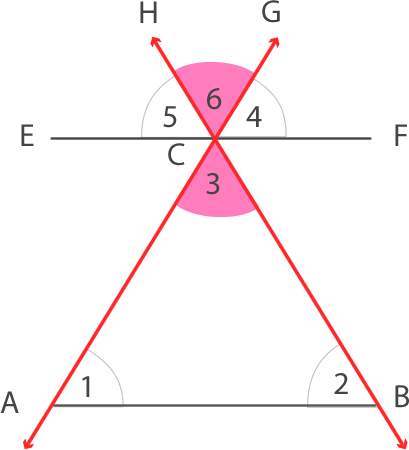
Los ángulos 3 y 6 son opuestos por el vértice, entonces tienen la misma medida.

Los ángulos 4, 5 y 6 forman un ángulo extendido y estos tienen las mismas medidas que los ángulos 1, 2 y 3 respectivamente.

Reemplazamos cada ángulo y obtenemos lo siguiente:

 

 

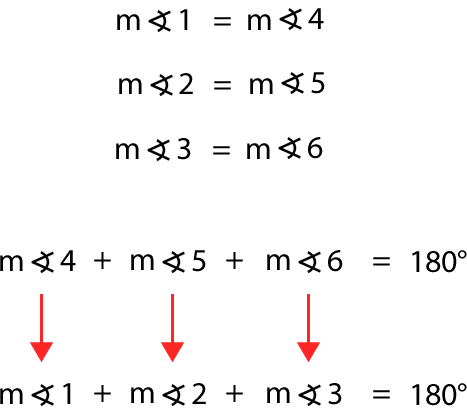
Con esto podemos comprobar que la suma de las medidas de los ángulos interiores de un triángulo es igual a 180°.

Para considerar:

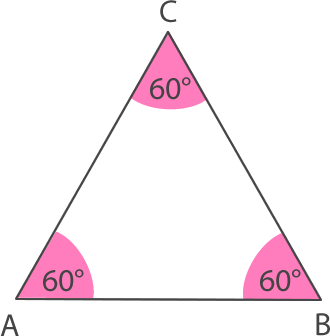
– Un triángulo equilátero tiene todos sus ángulos interiores de la misma medida. Cada uno mide 60°.

 

 

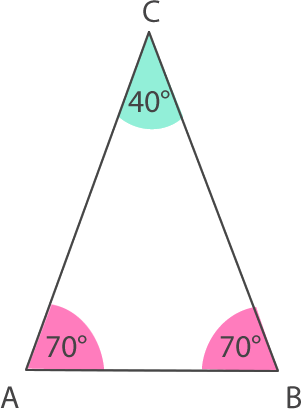
– En un triángulo isósceles los ángulos basales tienen la misma medida.
Ejemplo:

 

 

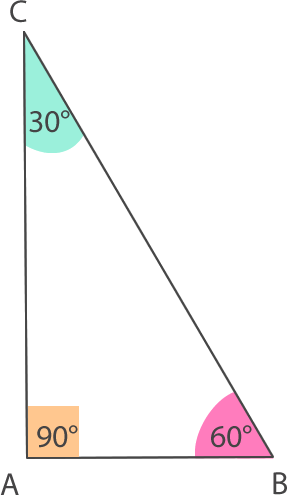
– En un triángulo escaleno sus tres ángulos interiores tienen distintas medidas.
Ejemplo:

 

1.3- Ejercicios resueltos
1.3.1- Calcula la medida de los ángulos interiores que falta en cada triángulo.
a)

 

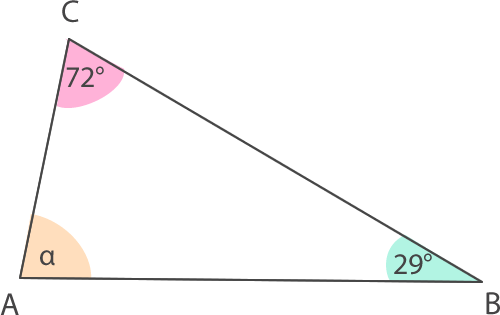
$$\begin{gathered} 72° + 29° + \alpha = 180° \\ 101°+ \alpha = 180° \\ \alpha = 180° – 101° \\ \alpha = 79° \end{gathered}$$

 

b)
 

 

$$\begin{gathered} 40° + 110° + \beta = 180° \\ 150°+ \beta = 180° \\ \beta = 180° – 150° \\ \beta = 30° \end{gathered}$$

 

c)
 

 

 

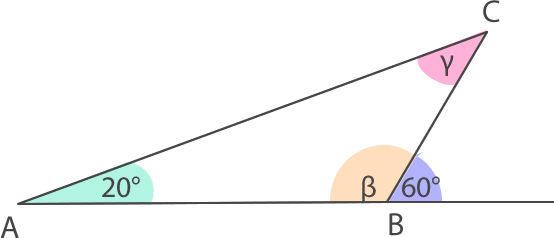
En este caso el ángulo $\beta$ sumado con 60° es igual a 180°, ya que son suplementarios. Entonces, podemos realizar el siguiente cálculo:

$$\begin{gathered} 60° + \beta = 180° \\ \beta = 180° – 60° \\ \beta = 120° \end{gathered}$$

 

A continuación, podemos calcular el valor de $\gamma$.

 

$$\begin{gathered} 20° + 120° +\gamma = 180° \\ 140°+ \gamma = 180° \\ \gamma = 180° – 140° \\ \gamma = 40° \end{gathered}$$

 

 

2- Ángulos en un cuadrilátero

Los cuadriláteros son polígonos de cuatro lados y cuatro ángulos. Los cuadriláteros tienen distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales.

Analicemos el siguiente caso:
En la imagen se muestra el cuadrilátero ABCD.

 

 

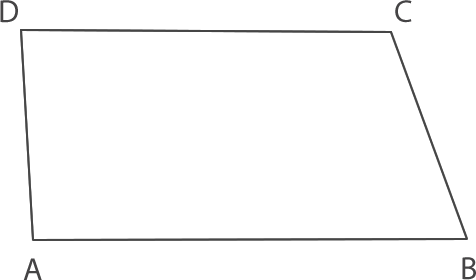
Luego, se trazó la diagonal AC. Como puedes ver la diagonal divide al cuadrilátero en dos triángulos.

 

 

Considerando que la suma de los ángulos interiores de un triángulo es 180°, entonces podemos concluir que la suma de los ángulos interiores de un cuadrilátero será dos veces la del triángulo, es decir, 360°.

En todos los cuadriláteros la suma de los ángulos interiores es igual a 360º.

Para considerar:
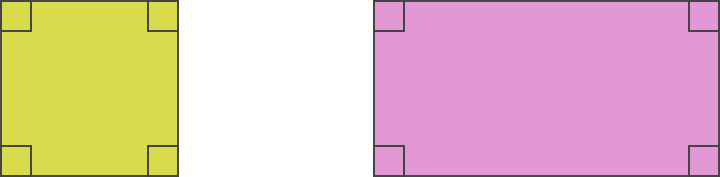
– El cuadrado tiene todos sus ángulos rectos, al igual que el rectángulo.

 

 

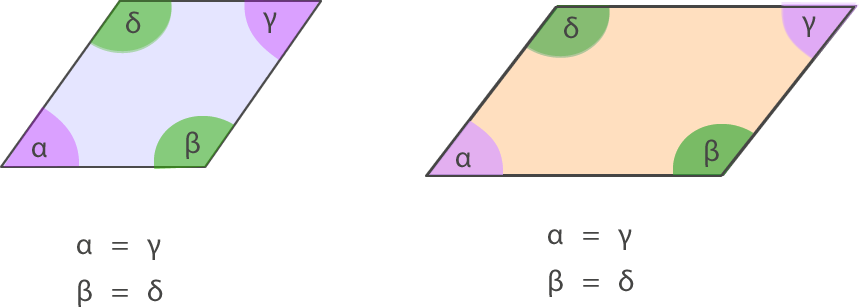
– Los ángulos opuestos del rombo y el romboide son congruentes, es decir, tienen la misma medida.

 

 

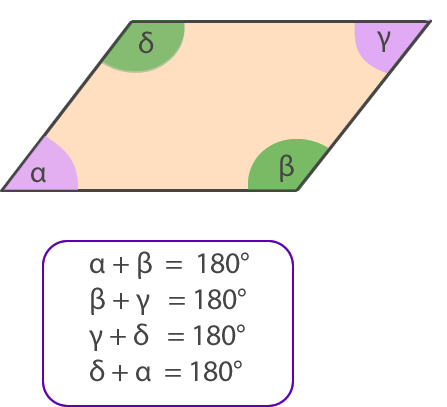
Los ángulos consecutivos de un paralelogramo (cuadrado, rectángulo, rombo y romboide) son suplementarios.

 

 

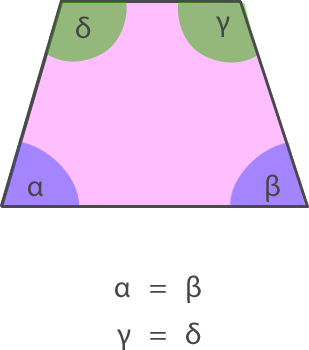
– El trapecio isósceles tiene sus ángulos basales congruentes entre sí.

 

 

2.1- Ejercicios resueltos
2.1.1- Determina las medidas de los ángulos que faltan en cada cuadrilátero:
a)

 

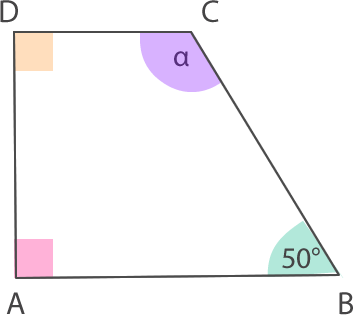
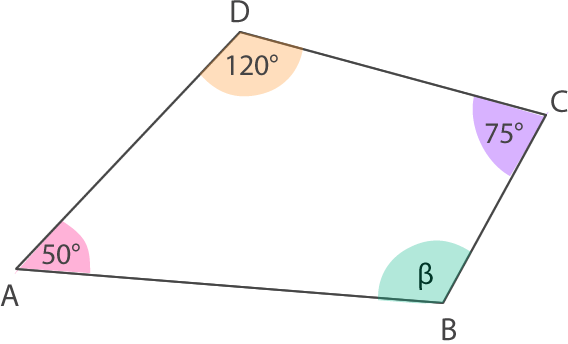
$$\begin{gathered} 90° + 90° + 50° + \alpha = 360° \\ 230°+ \alpha = 360° \\ \alpha = 360° – 230° \\ \alpha = 130° \end{gathered}$$

 

b)

 

$$\begin{gathered} 120° + 50° + 75° + \beta = 360° \\ 245°+ \beta = 360° \\ \beta = 360° – 245° \\ \beta = 115° \end{gathered}$$

 

c) ABCD es un paralelogramo.

 

 

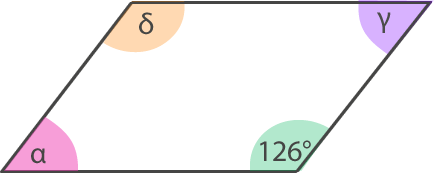
Para saber el valor de los ángulos desconocidos hay que considerar que los ángulos consecutivos de un paralelogramo son suplementarios.

 

$$\begin{gathered} 126° + \alpha = 180° \\ \alpha = 180° – 126° \\ \alpha = 54° \end{gathered}$$

$\alpha = \gamma$
 

Entonces $\gamma$ = 54°.

Por último, $\delta$ es opuesto a 126°.

$\delta$ = 126°.